딥러닝을 위한 통계 Chapter 1-1 ( 1-3 )

딥러닝을 위한 통계 Chapter 1-1

1. 확률 개요

1-1. 확률

• 확률이란, 특정한 사건이 일어날 가능성을 수로 표현한 것
• 확률은 0부터 1 사이의 실수로 표현된다.

1-2. 기계학습 모델을 확률적으로 이해하기

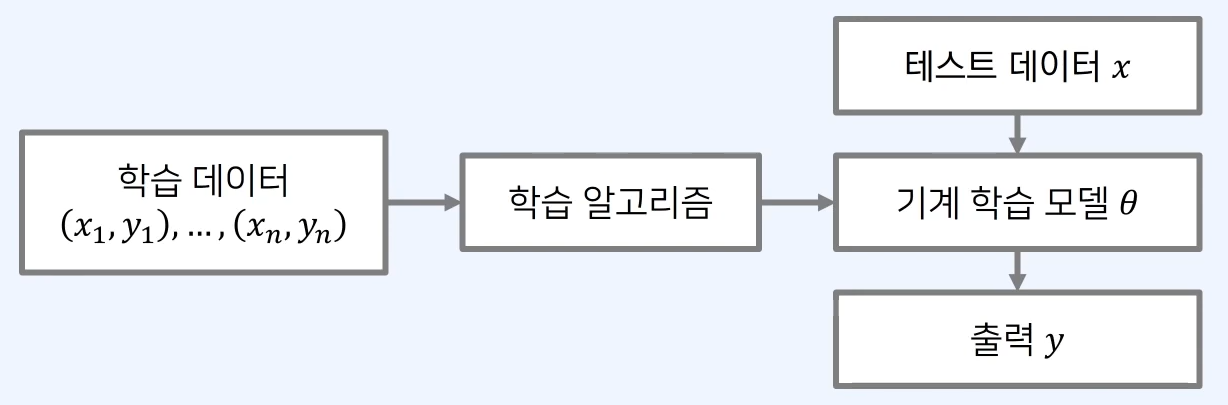
• 우리는 N개의 학습 데이터로 기계학습 모델을 학습한다.
• 일반적으로 기계학습 모델의 출력은 “확률” 형태를 띤다.

1-3. 경우의 수

• 경우의 수를 계산하는 방법으로는 순열(permutation)과 조합(combination)이 있다.

1-4. 순열과 조합

순열

• 서로 다른 n개에서 r개를 중복 없이 뽑아 특정한 순서로 나열한 것

1) $n = r$ 일때

\[_nP_r = n!\]

2) $n \neq r$ 일때

\[_nP_r = {n! \over (n-r)!}\]

• 0!은 1이다.

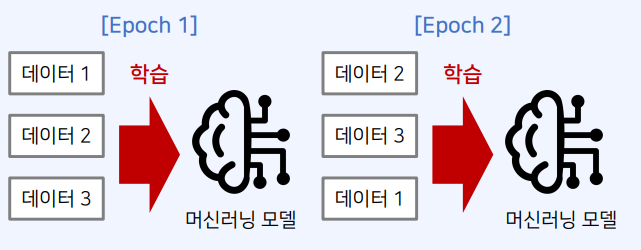
• 기계 학습 모델 학습을 위해 N개의 학습 데이터로 학습을 진행
• 이때 매번(epoch) 모델에 학습 데이터를 넣을 순서를 겄어서 학습을 진행
• 에포크(epoch) : 학습 데이터 세트에 포함된 모든 데이터가 한 번씩 모델을 통과한 횟수

from itertools import permutations

arr = ["A", "B", "C"]
# 원소 중에서 2개를 뽑는 모든 순열 계산

result = list(permutations(arr, 2))
print(result)

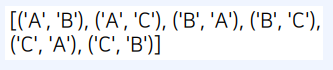
조합

• 서로 다른 n개에서 r개를 중복 없이 순서를 고려하지 않고 뽑는 것

\[_nC_r = {n! \over r!(n-r)!} = _nC_{n-r}\]

from itertools import combinations

arr = ["A", "B", "C"]
# 원소 중에서 2개를 뽑는 모든 조합 계산
result = list(combinations(arr, 2))
print(result)

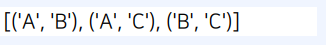
1-5. 중복 순열과 중복 조합

중복 순열

• 서로 다른 n개에서 중복을 포함해 r개를 뽑아 특정한 순서로 나열한 것

\[_nΠ_r = n^r\]

from itertools import product
arr = ['A'
, 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 중복 순열 계산
result = list(product(arr, repeat=2))
print(result)

중복 조합

• 서로 다른 𝑛개에서 중복을 포함해 순서를 고려하지 않고 𝑟개를 뽑는 것

\[_𝑛Η_𝑟 = _{𝑛+𝑟−1}𝐶_r\]

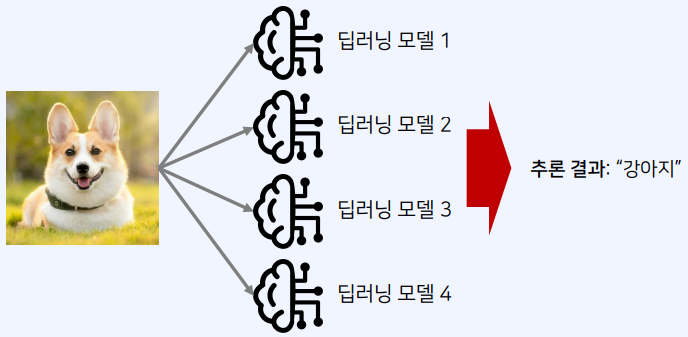
• 딥러닝에서는 학습된 여러 모델의 결과를 활용하여 최종적인 결과를 생성하는 앙상블(ensemble) 방법이 존재한다.

from itertools import combinations_with_replacement
arr = ['A'
, 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 중복 조합 계산
result = list(combinations_with_replacement(arr, 2))
print(result)

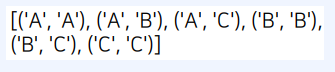
1-6. 확률과 통계적 확률

확률

• S를 전체 사건(event)의 집합(표본 공간 = sample space)라고 하자.
• 사건 X가 일어날 확률(probabilty) p(X)는 다음과 같다.
• p(X) = 사건 X가 일어나는 경우의 수/ 전체 경우의 수 = n(X)/n(S)

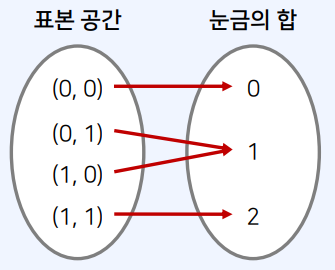
앞면에 1, 뒷면에 0이 쓰여 있는 2개의 동전을 2번 던졌을 때, 눈금의 합이 1일 확률은?

통계적 확률

• 동일한 시행을 𝑁번 반복해 사건 𝑋가 발생한 횟수를 𝑅이라고 하자.
• 시행 횟수 𝑁을 무한히 크게 만들었을 때, 𝑅/𝑁이 수렴하는 값을 사건 𝑋의 통계적 확률이라 한다.
• 프로그램을 이용해 많은 시행을 수행하여, 확률을 계산해 볼 수 있다.
• 목표 확률: 0.167

2. 확률 변수와 확률 분포

2-1. 시행(Trial)과 사건(Event)

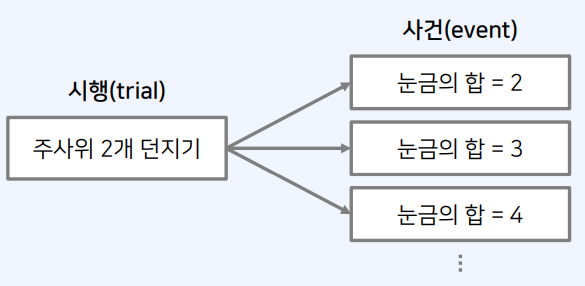
• 확률에 대하여 이해하기 위해서, 먼저 시행(trial)과 사건(event)에 대해 알아야 한다.
• 시행(trial): 반복할 수 있으며, 매번 결과가 달라질 수 있는 실험 ex) 주사위를 2개를 던지는 행동
• 사건(event): 시행에 따른 결과를 의미 ex) 눈금의 합이 7이 되는 사건

2-2. 확률 변수와 확률 함수

확률 변수

• 확률 변수란, 사건으로 인해 그 값이 확률적으로 정해지는 변수를 의미한다.
• 주사위 2개를 던지는 시행을 할 때마다 눈금의 합이 변할 수 있다.
• 따라서 “확률 변수 = 눈금의 합”으로 표현할 수 있다.
• 확률 변수는 대문자 𝑋로 표기하고, 확률 변수가 취할 수 있는 값은 소문자 𝑥로 표현한다.

확률 함수

• 앞서 확률 변수란, 시행할 때마다 변할 수 있는 값(눈금의 합)이라고 했다.
• 확률 함수란, 확률 변수에 따라서 확률 값을 부여하는 함수를 말한다.
• 확률 함수는 일반적으로 𝑃라고 표현한다.
• 주사위 두 개 던지기(시행)을 했을 때 눈금의 합이 3이 나올 확률은 2/36이다.
• 눈금의 합이 3이 되는 경우로는 (1, 2)와 (2, 1)의 두 가지 경우가 존재한다.
• $𝑃(𝑋 = 3) = 2/36$

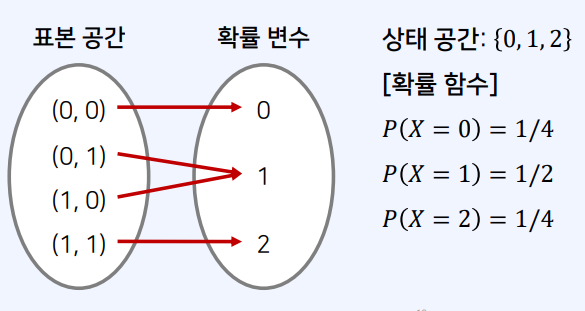
확률 변수 예시

• 2개의 동전을 던지는 시행에 대하여:
• 수학적으로, 각 사건에 대한 확률은 다음과 같이 표현할 수 있다.
• 눈금의 합이 0인 사건이 발생할 확률: $𝑃(𝑋 = 0) = 1/4$
• 눈금의 합이 1인 사건이 발생할 확률: $𝑃(𝑋 = 1) = 1/2$
• 눈금의 합이 2인 사건이 발생할 확률: $𝑃(𝑋 = 2) = 1/4$

2-3. 딥러닝 분야에서의 사건(Event)

• 우리가 흔히 얻을 수 있는 데이터는 사건(event)로 이해할 수 있다.
• 이미지 분류 모델을 학습할 때는 다양한 이미지를 사용한다.
• 이때 내가 수집하여 가지고 있는 이미지를 사건(event)으로 이해할 수 있다.

2-4. 확률 분포와 확률 분포 함수

확률 분포

• 각 사건에 어느 정도의 확률이 할당되었는지 표현한 정보를 의미한다.
• 확률 분포를 통해 통계적인 특성을 쉽게 이해할 수 있다.

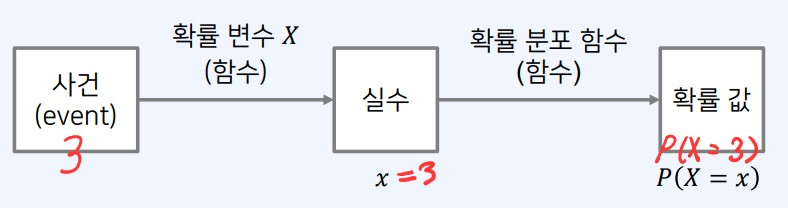
확률 분포 함수

• 확률변수 𝑋가 가지는 값 𝑥에 확률 𝑃 𝑋 = 𝑥 을 대응시키는 함수를 의미한다.
• [참고] 확률 분포 그 자체를 함수로 보고, 확률 분포 함수 𝑃와 같은 의미로 쓰기도 한다.
• 확률 분포 함수로 대표적인 것으로는 ① 확률질량함수, ② 확률밀도함수가 있다.
• 모든 사건에 대하여 확률 분포 함수의 값을 표현한 것을 “확률 분포”로 이해할 수 있다.

2-5. 이산확률분포와 확률질량함수

이산확률분포

• 확률변수 𝑋가 취할 수 있는 모든 값을 셀 수 있는 경우, 이를 이산확률변수라고 한다.
• 이때 이산확률분포는 이산확률변수의 확률 분포를 의미한다.
• 주사위를 던졌을 때 나올 수 있는 눈금은 {1, 2, 3, 4, 5, 6} 중 하나이다.
• 따라서, 이 경우 “주사위 눈금”의 값은 6개만 존재하므로, 이산확률변수이다.

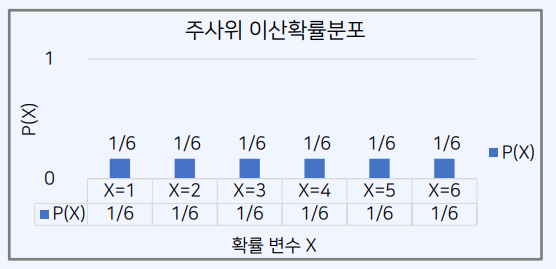
확률질량함수

• 확률질량함수는 이산확률변수가 특정한 값을 가질 확률을 출력하는 함수다.
• 확률질량함수는 이산확률분포를 표현하기 위해 사용하는 확률분포함수로 이해할 수 있다.
• 동전 2개를 동시에 던지는 시행에서 두 눈금의 합을 𝑋라고 하자.
• 이때, 𝑋는 이산확률변수로, 확률질량함수 𝑓 𝑥 는 다음과 같이 정의할 수 있다. $𝑓(0) = 𝑃(𝑋 = 0) = 1/4$ $𝑓(1) = 𝑃(𝑋 = 1) = 1/2$ $𝑓(2) = 𝑃 (𝑋 = 2) = 1/4$
• 확률 변수 𝑋에 대한 확률질량함수라는 의미로 𝑓𝑋 𝑥 라고 표기하기도 한다

예시 1)

• 딥러닝을 공부할 때, 확률 분포에 대해서 꼭 이해할 필요가 있다.
• 분류(classification) 모델의 출력은 확률 분포에 해당한다.
• 이미지 𝑥가 주어졌을 때 클래스 𝑦의 확률을 𝑃 𝑦 𝑥 로 표현할 수 있다.
• 확률 변수 𝑋의 값에 따라서 𝑌의 확률 분포가 변경된다는 의미에서 조건부 확률이라 한다.

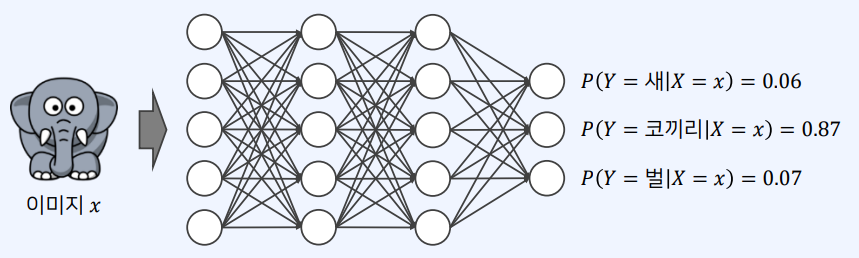
예시 2)

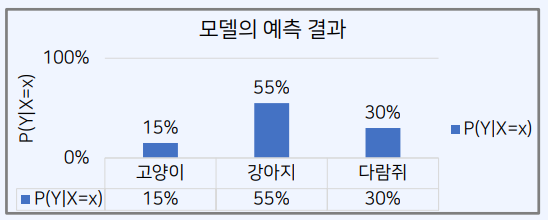
• 한 장의 이미지 𝑥가 주어졌을 때, 분류 모델의 실행 결과가 다음과 같다고 해보자.
• $𝑃 (𝑌 = 고양이 \mid 𝑋 = 𝑥) = 15\%$
• $𝑃 (𝑌 = 강아지 \mid 𝑋 = 𝑥) = 55\%$
• $𝑃 (𝑌 = 다람쥐\mid 𝑋 = 𝑥) = 30\%$

• $P(Y\mid X)$는 X값이 주어 졌을 때, 확률 변수 Y에 대한 확률 분포를 의미한다.
• 확률질량함수

2-6. 연속확률변수와 확률밀도함수

연속확률변수

• 확률변수 𝑋가 취할 수 있는 값이 무한한 경우, 이를 연속확률변수라고 한다.
• 연속적인 값의 예시: 키, 달리기 성적 등
• 이러한 경우 키가 170cm 이상, 175cm 미만일 확률을 구하는 방식을 사용할 수 있다.

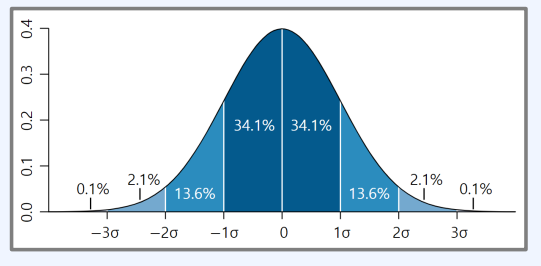
확률밀도함수

• 연속확률변수가 주어진 구간 내에 포함될 확률을 출력하는 함수다.

예시 1)

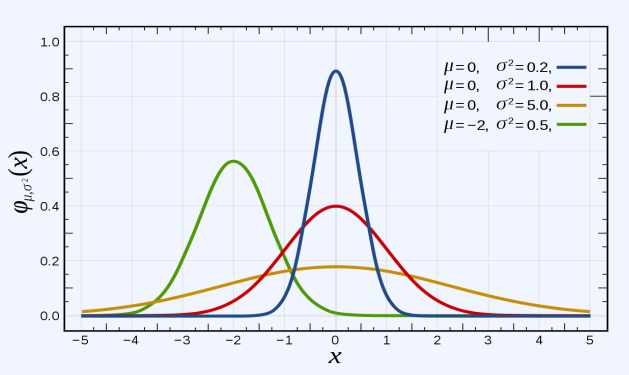
3. 이산확률분포

3-1. 베르누이 시행

• 결과가 두 가지 중 하나로만 나오는 시행
• 예시 1) 입학 시험 → 합격 혹은 불합격
• 베르누이 시행의 결과를 실수 0 혹은 1로 나타낸다.
• 확률 변수는 0 혹은 1의 값만 가질 수 있으므로, 이산확률변수다.

3-2. 베르누이 확률분포와 확률질량함수

베르누이 확률분포

• 베르누이 확률변수의 분포를 베르누이 확률분포라고 한다.
• 확률변수 𝑋가 베르누이 분포를 따른다고 표현하며, 수식으로는 다음과 같이 표현한다.

\[X\sim Bern(x;\mu)\]

• 모수(parameter)는 세미콜론(;) 기호로 구분하여 표기한다.
• 베르누이 확률분포는 모수로 𝜇(mu)를 가지는데, 1이 나올 확률을 의미한다.

베르누이 분포의 확률질량함수

\[Bern(x;\mu) = \begin{cases} \mu &\text{if } x=1 \\ 1 - \mu &\text{if } x=0 \end{cases}\]

이는 간단히 아래와 같은 하나의 수식으로 표현할 수 있다

\[Bern(x;\mu) = \mu^x(1-\mu)^{1-x}\]

𝜇가 0.8인 베르누이 확률 분포는 다음과 같다.

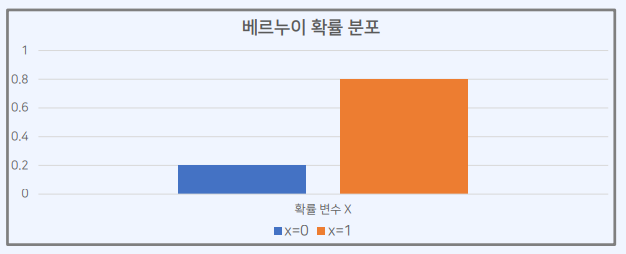
3-3. 이항 분포

• 성공 확률이 𝜇인 베르누이 시행을 𝑁번 반복한다.
• 𝑁번 중에서 성공한 횟수를 확률 변수 𝑋라고 하자.
• 𝑋는 0부터 𝑁까지의 정수 중 하나이다.
• 이러한 확률 변수를 이항 분포를 따른다고 한다

\[X\sim Bin(x; N, \mu)\]

• 이항 분포는 모수(parameter)로 𝑁과 𝜇를 가진다.
• 시행 횟수 𝑁

• 한 번의 횟수에서 1이 나올 확률 $\mu$

• 이항 분포 확률 변수 𝑋의 확률 질량 함수는 다음과 같다.

\[X\sim Bin(x; N, \mu) = \bigg(\begin{matrix} N\\x \end{matrix}\bigg)\mu^x(1-\mu)^{N-x}\]

• $\bigg(\begin{matrix} N\x \end{matrix}\bigg)$는 N개에서 x개를 선택하는 조합의 수와 같다.l

이항 분포 공식

• 독립된 사건을 𝑁번 반복 시행했을 때, 특정 사건이 𝑥회 발생한다고 가정한다.

예시 1)

[문제]

• 고양이 분류 딥러닝 모델 𝜃는 5개의 고양이 사진 중에 4개를 정확히 예측한다고 한다.
• • 모델에 10개의 고양이 사진을 주었을 때, 7개를 정확히 예측할 확률은 얼마일까?

[해설]

• 예측 성공 확률: 80%, 예측 실패 확률: 20% → 𝑝 = 80%
• 10개 중에서 7개를 정확히 예측해야 하는 것이므로, 다음과 같다.
• $\bigg(\begin{matrix} 10\7 \end{matrix}\bigg)p^7 \times (1-p)^3 = 0.2013$

예시 2)

[문제]

• 가구 공장에서 가구를 만들 때, 불량률이 10%라고 한다.
• 이 공장에서 만든 가구 10개를 확인했을 때, 불량품이 2개 이하로 나올 확률을 구하여라.
• 불량률 10% → 𝑝 = 10%

[해설]

• 불량품이 0개 나올 확률 + 불량품이 1개 나올 확률 + 불량품이 2개 나올 확률

$\bigg(\begin{matrix} 10\0 \end{matrix}\bigg)p^0 \times (1-p)^{10} + \bigg(\begin{matrix} 10\1 \end{matrix}\bigg)p^1 \times (1-p)^9 + \bigg(\begin{matrix} 10\2 \end{matrix}\bigg)p^2 \times (1-p)^8$

$= 0.3487 + 0.3974 + 0.1937 = 0.9298$

3-4 포아송 분포

• 일정한 시간 내 발생하는 사건의 발생 횟수에 대한 확률을 계산할 때 사용한다.
• 단위 시간에 어떤 사건이 발생할 기댓값이 𝜆일 때, 그 사건이 𝑥회 일어날 확률을 구할 수 있다.

\[f(x; \lambda) = \frac{e^{-\lambda}\lambda^x}{x!}\]

• 포아송 분포의 평균을 𝜆로 표기한다.
• 𝑒는 자연 상수를 의미한다. (𝑒 = 2.718 …)

예시 1)

단위 시간 내 평균 발생 횟수$(\lambda)$가 5일 때, 그 사건이 8회 일어날 확률은?

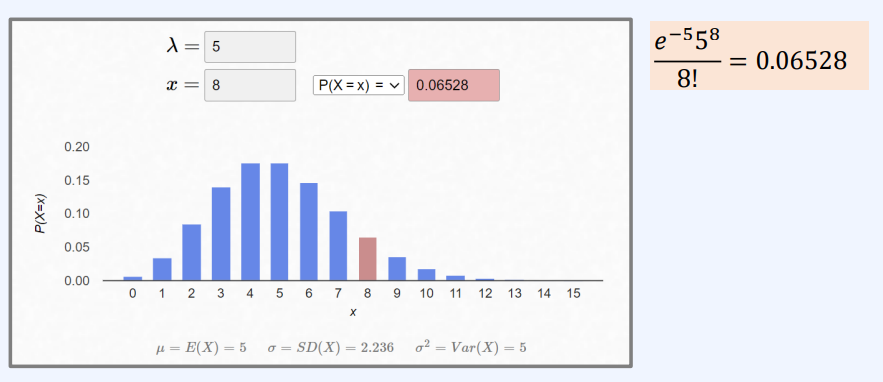
예시 2)

[문제]

• 하루에 평균적으로 5개의 스팸 메일이 도착한다.
  1. 오늘 하루 동안 스팸 메일이 1개 도착할 확률은 얼마일까?
  2. 오늘 하루 동안 스팸 메일이 5개 도착할 확률을 얼마일까?
  3. 오늘 하루 동안 스팸 메일이 8개 도착할 확률을 얼마일까?

[해설]

• 단위 시간에 스팸 메일이 5개 도착한다. 따라서 평균 발생 횟수(𝜆)는 5다.

\[f(x) = \frac{e^{-5}5^x}{x!}\]

1. 스팸 메일이 1개 도착할 확률: $f(x) = \frac{e^{-5}5^1}{1!} = 0.0337$
2. 스팸 메일이 5개 도착할 확률: $f(x) = \frac{e^{-5}5^5}{5!} = 0.1755$
3. 스팸 메일이 8개 도착할 확률: $f(x) = \frac{e^{-5}5^8}{8!} = 0.0653$