딥러닝을 위한 통계 Chapter 1-2 ( 4-6 )

딥러닝을 위한 통계 Chapter 1-2

1. 연속확률분포

• 확률변수 $X$가 취할 수 있는 값이 무한한 경우, 이를 연속확률변수라고 한다.
• 이때 연속확률분포는 연속확률변수의 확률 분포를 의미한다.

정규분포

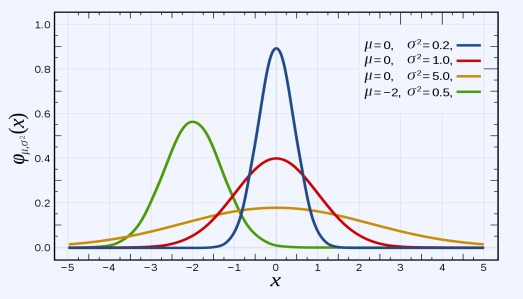
• 특정한 구간 $a \le x \le b$에 대한 확률로 표현한다.

1-1. 연속확률분포의 성질

• 확률 변수$X$가 어떠한 구간에 속할 확률은 -과 1사이이다. 그리고 값을 가질 수 있는 모든 구간의 화귤ㄹ을 합치면 1이다. 단, 각 구간은 배반(서로 겹치는 게 없을 때) 관계일 때 이것이 성립한다.

[해석]

1. $f(x)$는 확률을 의미, $dx$는 구간 길이
2. 확률밀도함수 $f(x)$가 주어졌을때 모든 범위의 x에 대해서 값은 1이다.

1-2. 균등 분포

• 가장 단순한 연속활률분포로, 특정 구간 내 값들이 나타날 가능성이 균등하다. 따라서 모든 확률변수에 대해 일정한 확률을 가지는 확률 분포
• $X$가 균등 분포를 따를 때 $X \sim U(a,b)$로 표현한다.
• 균등 분포를 따르는 확률 변수 $X$의 확률밀도함수는 다음과 같다. \(f(x) = \begin{cases} \frac{1}{b-a} &a \le X \le b \\ 0&otherwise \end{cases}\)

  예시

• 매일 오후 3시부터 오후 4시 사이에 하나의 스팸 메일이 도착
• 해당 시간 안에서 특정 시간에 스팸 메일이 도착할 확률이 동일하다고 가정
• 도착하는 시각은 확률변수 $X$
• 확률 분포 함수는 다음과 같이 그려짐

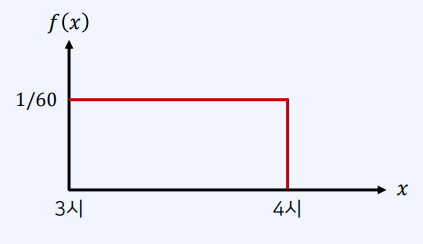
[해석]

1. 가로 축의 단위를 ‘분’으로 했을 때, 가로 길이가 60이다.
2. 오후 3시부터 4시 시간대의 각 분에 대하여 $f(x)$는 1/60이다.

---

[문제2]

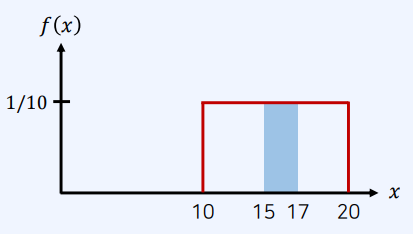
확률 변수 $X$가 구간 [10,20]에서 균등한 분포를 가질 때, $P(15 \le X \le 17)$은?

[풀이]

$X$의 확률 밀도 함수가 $f(x) = \frac{1}{20-10} = \frac{1}{10}$ 이므로, $P( 15\le X \le 17) = \frac {1}{10} \times 2=\frac{1}{5}$ 이다.

1-3. 정규 분포

• 현실 세계의 많은 데이터의 상당수가 정규 분포로 매우 가깝게 표현되는 경향이 있음
• 수집된 데이터의 분포를 근사할 때 자주 사용

특징

• 정규 분포의 모양은 평균과 표준편차로 결정
• 확률밀도함수는 평균을 중심으로 좌우 대칭인 종 모양을 형성
• 관측되는 값의 약 98%가 $\pm 2 \sigma$범위 안에 속함
• 평균에 따라서 정규 분포가 좌우로 평행이동함

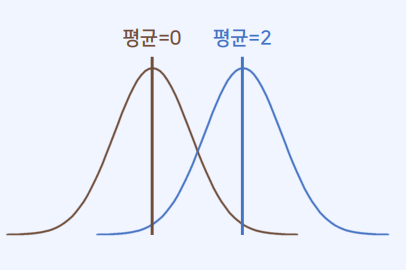
• 분산이 클수록 정규 분포가 옆으로 넓게 퍼짐

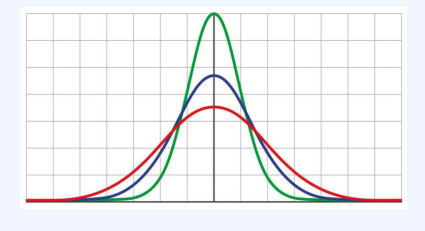
확률밀도함수

\(f(x) = \frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}\)

• 공학 분야에서는 가우시안 분포로 부르기도 함
• $\mu =$ 평균의 값
• $\sigma = $ 표준편차 ( $표준편차^2 = 분산$)

표준 정규 분포

• 평균이 0, 표준편차가 1인 정규분포
• 실제로는 정규 분포 함수를 표준 정규 분포로 변환한 뒤에 확률을 계산

1-4. 지수 분포

• 특정 시점에서 어떤 사건이 일어날 때까지 걸리는 시간을 측정할 때 사용

[문제] 한 명의 방문자가 접속한 뒤에, 그 다음 방문자가 올 때까지 걸리는 시간의 확률 구해보자. ( 웹 사이트에 평균적으로 10분에 한 명씩 방문자가 접속한다. )

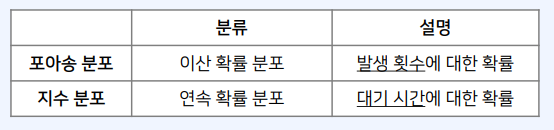
• 앞서 포아송 분포는 발생 횟수에 대한 확률을 구할 때 사용했다.
• 지수 분포는 대기 시간에 대한 확률을 구할 때 사용한다.

확률 밀도 함수 \(f(x) = \lambda e^{-\lambda x}, x \ge 0\)

• $\lambda$ : 단위 시간 동안 평균 사건 발생 횟수

[문제]

• 운영 중인 서버에는 하루 평균 4건의 해킹이 시도된다.
• 첫 번째 해킹 시도가 3시간 안에 발생할 확률은?

[해설]

• 24시간에 4건의 해킹이 발생하므로, 단위 시간이 “시간(hour)“일 때 평균 발생 횟수는 4/24다.

• 따라서, $\lambda = 4/24$이며, 확률 밀도 함수는 다음과 같다. \(f(t) = \frac{4}{24}e^{-\frac{4}{24}t}, t \ge 0\)

• 적분하여 계산하면 \(\int_{0}^{3} \bigg(-\frac{4}{24}\bigg)dt \\ = \bigg[-\exp\bigg(-\frac{4}{24}t\bigg)\bigg]^{3}_{0}\\ = \exp(0) - \exp\bigg(-\frac{4}{24} \times 3\bigg) = 0.3935\)

특성 - 무기억성

• 특정 시점에서부터 소요되는 시간은 과거로부터 영향을 받지 않음
• 예를 들어, 서버를 3년간 운영한 뒤, 해킹당하기까지 걸리는 시간은 처음 서버를 운영한 뒤 해킹당하기까지걸리는 시간과 같다.
• 한계점 : 현실 시계에서의 다양한 사례를 모델링하기에는 지나치게 단순한 경향이 있음

1-5. 데이터에 대한 확률 분포

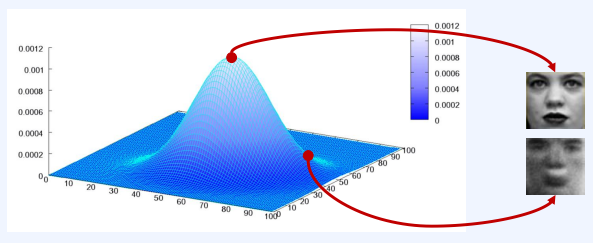
• 생성 모델 : 이미지의 분포를 근사해, 있을 법한 이미지를 생성할 수 있다.
• 사람의 걸굴에는 통계적인 평균치가 존재할 수 있다.

2. 표준정규분포

• 평균이 0이고 분산이 1인 표준화된 정규 분포

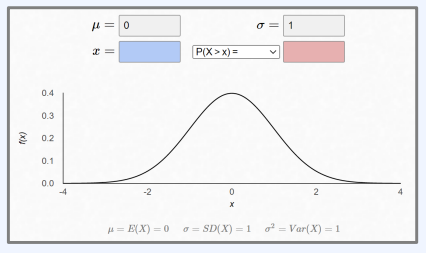
• 확률 변수 $X$가 $X \sim(\mu, \sigma^2)$를 따를 때, 다음의 공식으로 표준화를 할 수 있다. \(Z = \frac{X-\mu}{\sigma}\)

---

• 확률 변수 $Z$가 평균이 0이고 분산이 1인 정규분포
• $Z \sim N(0,1)$로 표현

• 확률밀도함수는 다음과 같음 \(f(Z) = \frac{1}{\sqrt {2\pi}}e^{-\frac{1}{2}Z^2}\) —

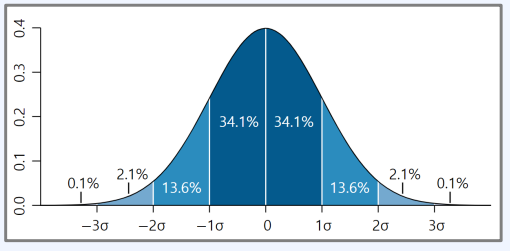
• 정규 분포의 확률을 계산할 때는 다음의 그림을 참고
• 표준 정규 분포의 경우 $\sigma$의 값이 1이므로, $P(Z \le 1)$ 을 약 84.1%로 볼 수 있다

누적 분포 함수

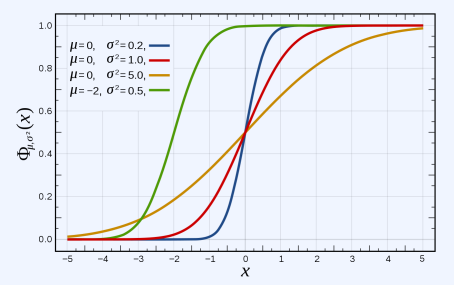
표준 정규 분포 표

• 정규 분포의 누적 분포 함수 값에 대한 표
• 미리 계산된 값임

• 사용한 예시
• 표준 정규 분포에서 $𝑃 (0 \le 𝑧 \le 0.75)$ 는 얼마일까?
• $𝑃 (0 \le 𝑧 \le 0.75)$ = $𝑃 (𝑧 \le 0.75) − 𝑃(𝑧 \le 0) = $ 0.77337 − 0.5 = 0.27337

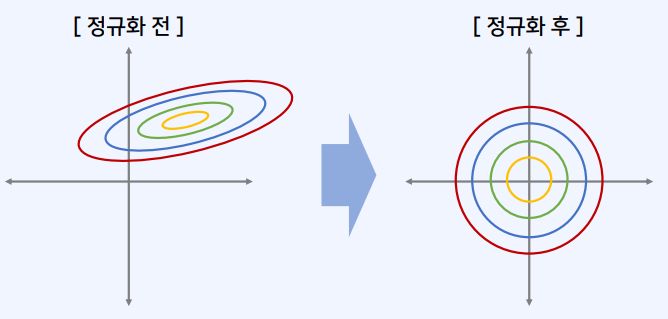
2-1. 딥러닝 분야의 입력 정규화

• 입력 데이터를 정규화하여 학습 속도를 개선할 수 있음

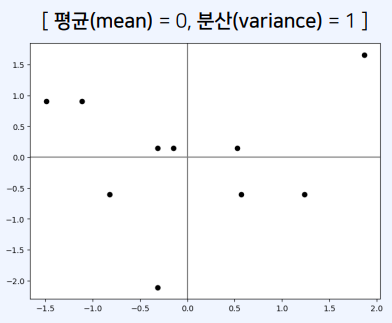
• 입력 데이터가 $N(0,1)$ 분포를 따르도록 표준화하는 예제는 다음과 같음

\[\hat x = \frac{x-E[x]}{\sqrt{Var[x]}}\]

x1 = np.asarray([33, 72, 40, 104, 52, 56, 89, 24, 52, 73])
x2 = np.asarray([9, 8, 7, 10, 5, 8, 7, 9, 8, 7])
normalized_x1 = (x1 - np.mean(x1)) / np.std(x1)
normalized_x2 = (x2 - np.mean(x2)) / np.std(x2)
plt.axvline(x=0, color='gray')
plt.axhline(y=0, color='gray')
plt.scatter(normalized_x1, normalized_x2, color='black')
plt.show()

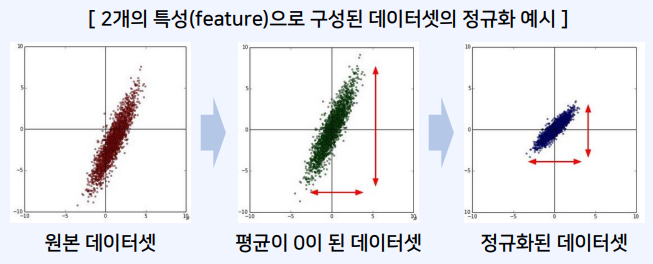
• 입력 정규화를 이용해 각 차원의 데이터가 동일한 범위 내의 값을 갖도록 만들 수 있음
• 모든 특성에 대하여 각각 평균만큼 빼고 특정 범위의 값을 갖도록 조절할 수 있음

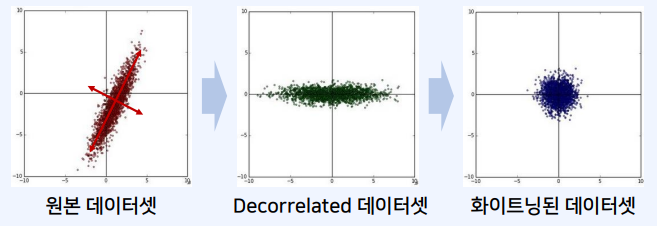
• 화이트닝은 평균이 0이며 공분산이 당위행렬인 정규분포 형태의 데이터로 변환함
• 일반적으로 딥러닝 분야에서는 PCA나 화이트닝보다는 정규화가 더 많이 사용됨

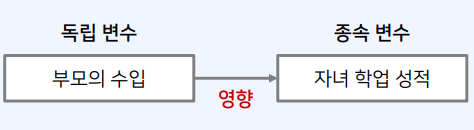
3. 독립 변수와 종속 변수

3-1. 변수와 가설

• 현실 세계에서는 하나의 변수가 다른 변수에 영향을 미치는 경우가 많음
• 예시 1) 부모의 수입이 높으면, 자녀의 학업 성적이 우수할까?
• 예시 2) 가족 구성원의 수가 많을수록, 가정 내 한 달 평균 식비가 높을까?

3-2. 독립 변수

• 독립 : 다른 변수에 의하여 영향을 받지 않는 변수
• 종속 변수에 영향을 주는 변수
• 독립 변수는 연구자가 마음대로 조정 가능

3-3. 종속 변수

• 독립 변수에 영향을 받아 변화하는 변수를 종속 변수
• 용어가 다양함

분류 모델

• 독립 변수 = 이미지 $x$
• 종속 변수 = 추론 결과 $y$

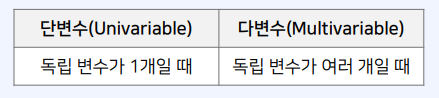
3-4. 변수와 변량

• 변수는 독립변수 $X$를 의미

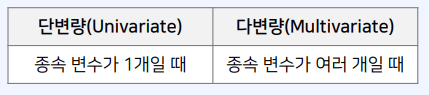
• 변량은 종속변수 $Y$를 의미

예시

• 회귀 문제의 경우
• ① 노동 시간, ② 종업원의 수, ③ 가게의 크기에 따라서 매출액을 예상
• 독립 변수가 (노동 시간, 종업원의 수, 가게의 크기) 3개
• 종속 변수가 (매출액) 1개