딥러닝을 위한 통계 Chapter 1-3 ( 7-8 )

딥러닝을 위한 통계 Chapter 1-3

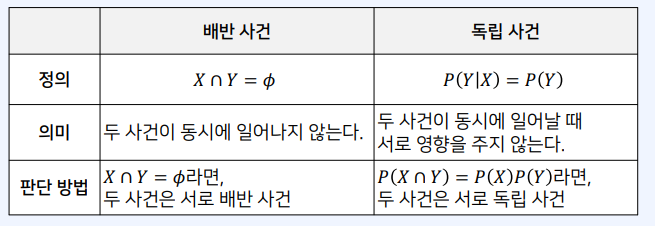
1. 결합 확률과 주변 확률

1-1. 독립과 종속

독립

• $P(X \cap Y) = P(X)P(Y)$인 경우, 두 사건 $X$와$Y$는 서로 독립 ( 필요충분조건 )
• 두 변수가 서로 영향을 주지 않는다는 의미

종속

• 한 사건의 결과가 다른 사건에 영향을 주는 것

1-2. 배반 사건

• “교집합이 없는” 사건을 의미

배반 vs 독립

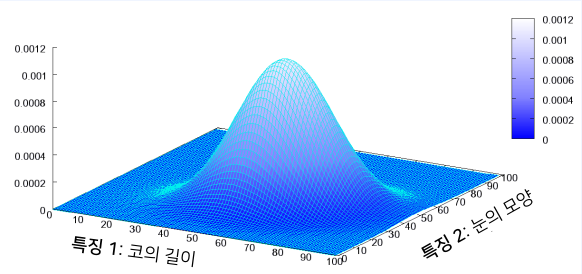
1-3. 다변수 확률 변수

• 확률 변수가 두개 이상 있는 경우
• 딥러닝 분야 분포는 일반적으로 다변수 확률 분포에 해당
• 아래는 얼굴 특징에 대한 확률 분포 예시

1-4. 결합 확률

• 두 개의 사건이 동시에 일어날 확률, 두 확률 변수의 교집합이 발생할 확률
• $P(X,Y)$ 혹은 $P(X \cap Y)$로 표현

결합 확률 함수

• 이산확률 변수 $X,Y$에 대한 결합 확률 함수 $f_{XY}(x_i,y_j)$란 무엇일까?

[특징]

• $f_{XY}(x_i,y_j) = P(X = x_i, Y=y_j)$
• $X$는 $x_1, x_2 \ldots$의 값을 가질 수 있고 $Y$는 $y_1, y_2 \ldots$의 값을 가질 수 있다고 가정
• 단순히 $f(x,y)$ 로 사용하기도 함

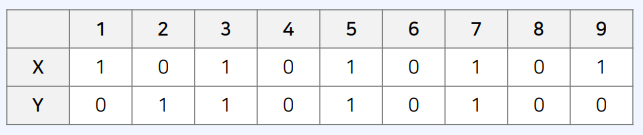
결합 확률 함수 예시

• 랜덤으로 1부터 9까지의 수 중에서 하나를 출력하는 기계
  1. 얻은 수가 짝수이면 $X = 0$, 홀수이면 $X = 1$
  2. 얻은 수가 소수가 아니면 $Y = 0$, 소수이면 $Y = 1$이다
• 얻을 수 있는 수에 따른 $X$와 $Y$의 값

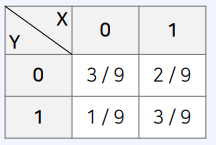
• 결합 확률 함수는
• $f 0,0 = 3/9$
• $f 0,1 = 1/9$
• $f 1,0 = 2/9$
• $f 1,1 = 3/9$

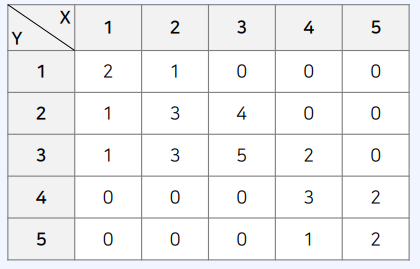
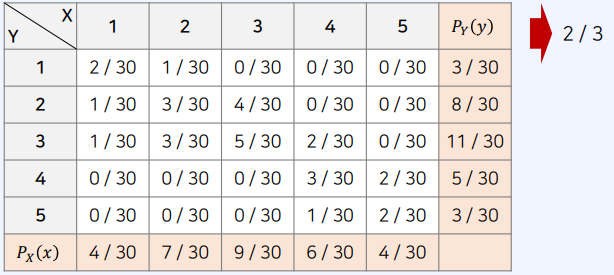
• 수학 점수는 등급 형태로 1부터 5까지의 값을 가짐
• 영어 점수는 등급 형태로 1부터 5까지의 값을 가짐
• 수학 등급 확률 변수 $X$
• 영어 등급 확률 변수 $Y$

[궁금한 점] 수학 등급이 높으면, 영어 등급도 높을까? → 결합 확률 분포를 확인하여 경향을 확인

• 테이블의 각 원소를 수학등급$(X)$이 $x$, 영어등급$(Y)$이 y인 학생의 수라고 가정

1-5. 결합확률질량함수와 주변확률질량함수

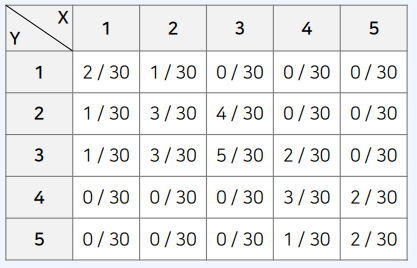
결합확률질량함수

• 확률은 $f_{XY}(x,y) = P(X = x, Y=y)$
• $\sum_i\sum_j P(X = x, Y = y) = 1$
• 전체 학생 수가 30명일 때, 수학이 1등급이면서 영어가 2등급인 학생이 1명 있다면?
• $P_{XY}(1,2) = P(X = 1, Y = 2) = 1/30$

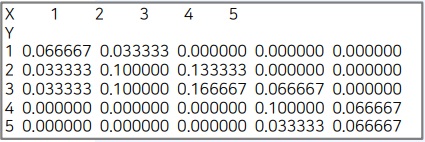
python 예시

import pandas as pd
scores = [1, 2, 3, 4, 5]
data = [
[2, 1, 0, 0, 0],
[1, 3, 4, 0, 0],
[1, 3, 5, 2, 0],
[0, 0, 0, 3, 2],
[0, 0, 0, 1, 2]
]
df = pd.DataFrame(data, index=scores, columns=scores)
df.columns.name = "X"
df.index.name = "Y"
pmf = df / df.values.sum()
print(pmf)

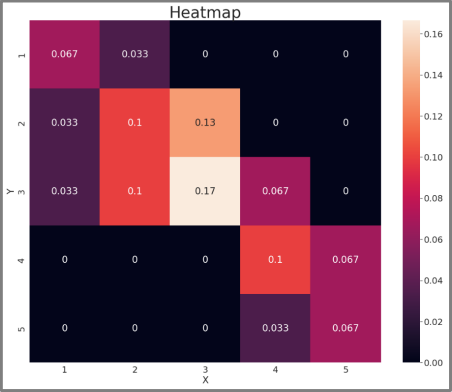
python 히트맵 예시

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(font_scale=2)
plt.rcParams["figure.figsize"] = [20, 16]
ax = sns.heatmap(pmf, annot=True,
xticklabels=[1, 2, 3, 4, 5],
yticklabels=[1, 2, 3, 4, 5]
)
plt.title("Heatmap"
, fontsize=40)
plt.show()

주변확률질량함수

• 두 확률 변수 중에서 하나의 확률 변수에 대해서만 확률 분포를 나타낸 함수
• $P_X(x) = \sum_{yi}P_{XY}(x,y_i)$
• $P_Y(y) = \sum_{xi}P_{XY}(x_i,y)$
• 수학 등급(X)가 1등급일 확률은 $P_X(1) = p_{XY}(1,1) + p_{XY}(1,2) + p_{XY}(1,3) + p_{XY}(1,4) + p_{XY}(1,5)$
• 즉, $X=1$로 고정하고, 모든 $Y$ 변수에 대하여 확률 값을 더한 것

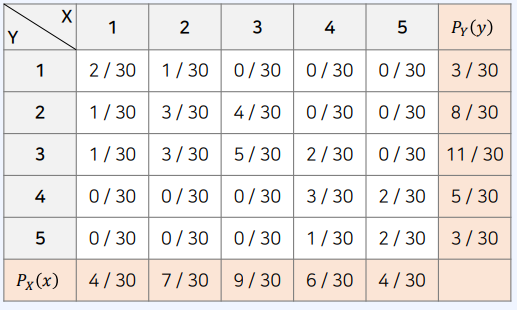
python 예시

index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index])
plt.xticks(x, ["1","2","3","4","5"])
plt.title(f"P(X, Y={index + 1})")
plt.show()

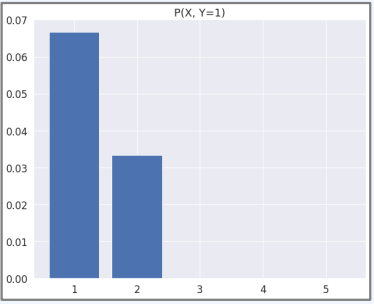
marginal_pmf_x = pmf.sum(axis=0)
print(marginal_pmf_x)
marginal_pmf_y = pmf.sum(axis=1)
print(marginal_pmf_y)

2. 조건부 확률

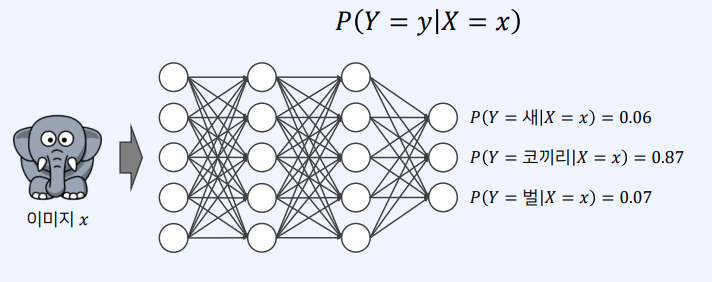
• 어떠한 사건이 일어나는 경우에 다른 사건이 일어날 확률
• 딥러닝 분야에서는 “$X$ 사건이 단서로 주어졌을 때, $Y$ 사건이 발생할 확률”

예시 1

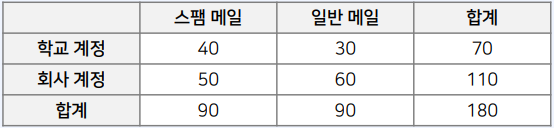
• 하나의 메일을 뽑았을 때, 학교 계정으로 온 메일일 확률

→ $𝑃(학교)$ = 70/180

• 하나의 메일을 뽑았을 때, 학교 계정으로 온 메일이면서 스팸 메일일 확률 (결합 확률)

→ $𝑃(학교 ∩ 스팸)$ = 40/180

• 스팸 메일 중 하나를 뽑았을 때, 학교 계정으로 온 메일을 확률 (조건부 확률)

→ $𝑷 (학교\mid 스팸)$ = 40/90

예시 2

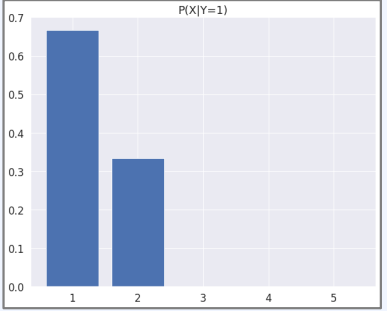
• 조건부 확률 질량 함수 공식은 $P_{Y\mid X}(y\mid x) = \frac{P_{XY}(x,y)}{P_X(x)}$
• 영어 성정$(Y)$이 1등급일 때, 수학 성적(X)이 1등급일 확률은?

python 예시

index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index] / marginal_pmf_y[index + 1])
plt.xticks(x, ["1", "2", "3", "4", "5"])
plt.title(f"P(X\mid Y={index + 1})")
plt.show()