딥러닝을 위한 통계 Chapter 1-4 ( 9-10 )

딥러닝을 위한 통계 Chapter 1-4

1. 베이즈 정리

1-1. 스팸 분류 모델

• 입력 : 하나의 텍스트
• 출력 : 텍스트가 특정 클래스에 속할 확률
• 목표 : 하나의 텍스트 $x$가 스팸 $y$일 확률 계산

• 텍스트의 확률 변수 $X$, 클래스의 확률 변수 $Y$
• 클래스는 2개만 존재

데이터를 분석할 결과

• 지금까지 받은 메일을 확인해 보았더니, 70%는 스팸, 30%는 정상
• 스팸 메일 중에 90%는 “대출”이라는 단어가 포함
• 정상 메일 중에 3%는 “대출”이라는 단어가 포함

Q. 이때, “대출”이라는 단어가 들어있는 메일이 스팸 메일일 확률을 구해보자

• $ P(Y\mid X) $를 계산할 수 있으면, 우리가 원하는 프로그램을 만들 수 있음

베이즈 정리

• 조건부확률을 구하는 공식
• $ P(A\mid B) = \frac{P(B\mid A)P(A)}{P(B)} $

다시 데이터를 분석한 결과를 위 공식으로 나타내면

• $𝑃(스팸)$ = 0.7
• $𝑃(정상)$ = 0.3
• $ 𝑃(대출\mid 스팸) $ = 0.9
• $𝑃(대출\mid 정상)$ = 0.03
• [알고자 하는 것] $𝑃(스팸\mid 대출)$
• 베이즈 정리에 따르면, $𝑃(스팸\mid 대출) = 𝑃(대출\mid 스팸)𝑃(스팸)/𝑃(대출)$
• 따라서 먼저 $𝑃(대출)$을 구하면

$𝑃(대출) = 𝑃 (대출 \cap 스팸) + 𝑃 (대출 \cap 정상)
= 𝑃 (대출\mid 스팸) 𝑃 (스팸) + 𝑃 (대출\mid 정상) 𝑃 (정상)
= 0.9 ∗ 0.7 + 0.03 ∗ 0.3 = 0.639$

[정답]

$𝑃(스팸\mid 대출) = 𝑃(대출\mid 스팸) 𝑃(스팸)/𝑃(대출)$ = 0.9 * 0.7 / 0.639

1-2. 확률 모델

• 일반적인 분류 모델 $ P(y\mid x) $는 다음과 같은 공식으로 예측 결과 $\hat y$를 계산
• $ \hat y = argmax_y P(y\mid x) $

($argmax_y$는 뒤 수식의 값이 최대가 되는 $y$를 찾겠다는 뜻)

1-3. 최대 우도(가능도) 추정

• 가능도(likelihood)가 가장 높은 클래스를 선택하는 방법
• $X$는 특징 혹은 데이터
• $ X = $광고성 단어의 개수로 가정하면 아래 예시에서는 $ X \ge 5$라면 스팸으로 분류

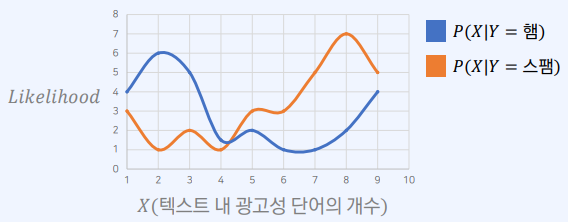
유의할 점

• 사후 확률을 직접적으로 계산하기 어렵기 때문에 가능도를 이용

• 하지만 가능도만으로 사후확률을 완전히 근사할 수 없음

• 전체 메일 중에서 스팸 메일의 수 자체가 적다고 가정
• $𝑃(𝑌 = 스팸) = 1/3$, $𝑃(𝑌 = 햄) = 2/3$
• 분포는 다음처럼 바뀜

• 이제는 $ X \ge 6 $ 이라면 스팸으로 분류

1-4. 베이즈 정리

• 정리하면, prior를 고려할 때 posterior를 더욱 잘 계산할 수 있음
• 베이즈 정리는 머신러닝 분야에서 끊임없이 등장하는 개념이므로 중요
• 나이브 베이즈 분류기 (Naïve Bayes Classifier)에서 사용
• 최신 인공지능 기술보다 성능은 많이 뒤떨어지지만 기본적인 모델로 자주 언급됨

2. 평균과 기댓값

2-1. 평균

• 다양한 종류가 있으며, 가장 일반적인 평균은 산술 평균
• 모든 관측 값을 더해 관측 값의 개수로 나눈 것 \(A = \frac{1}{n}\sum_{i=1}^na_i = \frac{a_1+a_2+\cdots a_n}{n}\)

계산 예시

• 5명의 학생의 딥러닝 강의 중간고사 점수가 각각 56, 93, 88, 72, 65점이다.
• 점수의 평균: (56 + 93 + 88 + 72 + 65) / 5 = 74.80

평균은 특정한 데이터 집단을 대표하기에 적절하지 않은 경우도 있음

2-2. 중앙값

• 주어진 값들을 순서대로 정렬했을 때, 가장 중앙에 위치하는 값

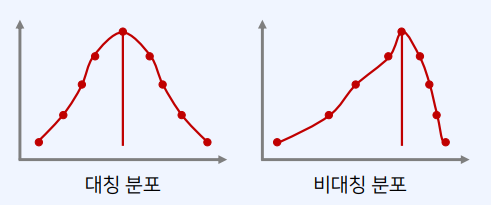
평균 vs 중앙값

• 평균: 데이터의 분포가 정규분포처럼 대칭적인 경우
• 중앙값: 데이터의 분포가 한쪽으로 치우쳐졌거나(skewed), 이상치(outlier)가 존재하는 경우

2-3. 기댓값

• 각 사건에 대해 확률 별수와 확률 값을 곱하여 전체 사건에 대하여 모두 더한 값
• $E[X] = \sum_i{(i번째 사건이 발생할 확률) \times (i번째 사건에 대한 확률 변수)}$
• 모든 사건에 대해 확률을 곱하면서 더하여 계산할 수 있음
• 이산확률변수에 대한 기댓값은 \(E[X] = \sum_i x_i \cdot f(x_i)\)
• 연속확률변수에 대한 기댓값은 \(E[X] = \int_{-\infty}^\infty x\cdot f(x)dx\)

평균 vs 기댓값

• 기댓값: 새로운 데이터가 관측되었을 때, 그 데이터가 확률적으로 어떤 값을 가질지를 예측할 때
• 평균: 이미 구해진 값에 대하여 통계적인 특성을 분석할 때

기댓값 예시 1

• 1000원 짜리 복권가 있을 때 기대 이익은?

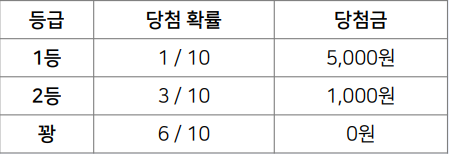
• $𝑃 [𝑋 = 5000] = 1/10$
• $𝑃 [𝑋 = 1000] = 3/10$
• $𝑃 [𝑋 = 0] = 6/10$

→ $(5,000 × 1/10) + (1,000 × 3/10) + (0 × 6/10) = 800원$

• 기대 이익은 $-200원$

기댓값 예시 2

• 특정한 사람 얼굴 이미지 𝑥가 주어진 상황을 가정
• 얼굴의 나이를 예측하는 모델 $𝑓(𝑥)$ 는 10세부터 13세 범위의 나이에 대해 확률을 예측
• 해당 모델이 예측한 결과 $𝑃(y\mid x)$ 는 다음과 같다.

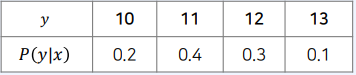
• 이때 기댓값을 계산한다면?

→ $(10 × 0.2) + (11 × 0.4) + (12 × 0.3) + (13 × 0.1) = 11.3$