딥러닝을 위한 통계 Chapter 1-5 ( 11-12 )

딥러닝을 위한 통계 Chapter 1-5

1. 분산과 표준 편차

1-1. 분산과 표준 편차

분산

• 평균과 관측치에 대하여 편차제곱의 평균 값을 의미
• $N$개의 데이터의 평균 값 $\mu$가 주어졌을 때, 분산은 다은의 공식으로 계산

분산의 공식 = $\frac{1}{N}\sum^N_{i=1}\mid x_i-\mu\mid ^2$

분산을 사용하는 이유

• 편차는 평균과의 차이이므로, 편차를 모두 더하면 단순히 0이 되므로 제곱하여 더함

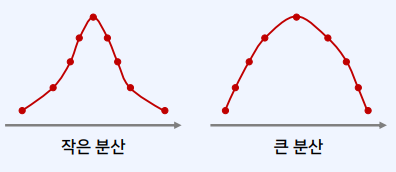
표준편차

• 표준편차는 분산의 양의 제곱근

표준 편차의 공식 = $\sqrt{\frac{1}{N}\sum^N _{i=1} \mid x_i - \mu\mid ^2}$

예시 1

예시 2

코드 실습

import math
arr = [56, 93, 88, 72, 65]
mean = 0
for x in arr:
mean += x / len(arr)
variance = 0
for x in arr:
variance += ((x - mean) ** 2) / len(arr)
std = math.sqrt(variance)
print(f"평균: {mean:.2f}")
print(f"분산: {variance:.2f}")
print(f"표준 편차: {std:.2f}")

2. 공분산과 상관계수

2-1. 공분산

• 변수가 여러 개 일 때의 분산은 어떻게 계산할 수 있을까?

공분산의 공식 = $s_{xy} = \frac{1}{N}\sum^N _{i=1}(x_i - \mu _x)(y_i - \mu _y)$

• 분산과 마찬가지로, 데이터가 평균으로부터 얼마나 멀리 떨어져 있는지를 나타냄
• 평균값의 위치와 표본 위치 사이의 사각형 면적을 사용

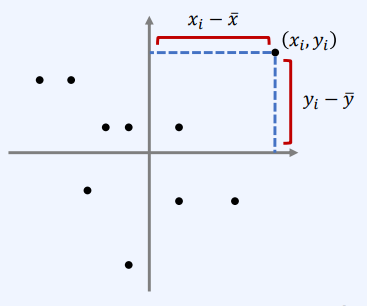
• 공분산의 크기 : 원점에서 얼마나 멀리 떨어져 있는지 알 수 있음
• 공분산의 방향 : 양수/음수에 따라 어느 방향을 가지는지 알 수 있음

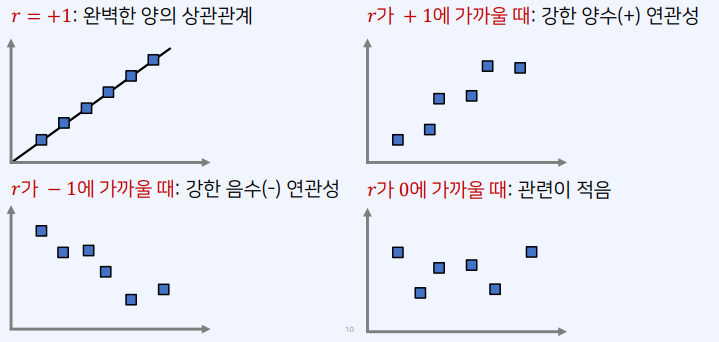
2-2. 상관계수

• 공분산에서 방향성(상관성)을 볼때 아래의 공식을 이용해 정규화를 진행할 수 있음

• 상관계수는 항상 -1 이상, 1 이하의 값을 가짐

• $S^2x$ = x의 분산 $S^2_y$ = y의 분산 $S{xy}$ = x와y의 공분산

$r_{xy} = \frac{S_{xy}}{\sqrt{S^2_x \cdot S62_y}}$

• 이를 피어슨 상관계수라고도 함

2-3. 공분산 행렬

• 기계학습 분야에서는 다변수 확률변수를 가정하는 경우가 많음
• 예를 들어 얼굴을 세 개의 특징으로 표현하고 이러한 데이터가 N개가 있다고 가정
• 다음과 같은 행렬이 완성됨

\[X =\begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{12} & x_{22} & x_{23} \\ x_{13} & x_{23} & x_{33} \\ & \vdots & \\ x_{N1} & x_{N2} & x_{n3} \\ \end{bmatrix}\]

• 이 행렬에서 모든 조합에 대하여 공분산을 한꺼번에 표기할 수 있음

\[X =\begin{bmatrix} \sigma_{x_1}^2 & \sigma_{x_1x_2} & \sigma_{x_1x_3} \\ \sigma_{x_1x_2} & \sigma_{x_2}^2 & \sigma_{x_2x_3} \\ \sigma_{x_1x_3} & \sigma_{x_2x_3} & \sigma_{x_3}^2 \\ \end{bmatrix}\]

특징

• 대각 선분은 각 확률변수의 분산
• 비 대각 성분은 두 확률변수의 공분산
• 두 확률 변수가 독립이라면, 공분산은 0

예시

1. 두 데이터가 양의 상관관계를 가지는 경우
   • 확률 변수 X의 값이 크면, Y의 값도 큰 경우를 의미

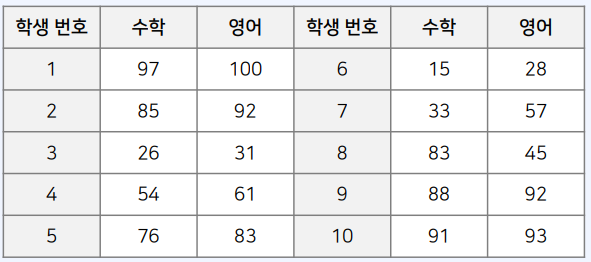
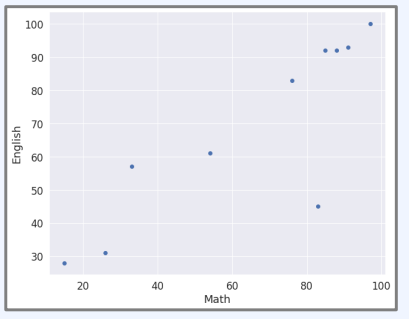
• 수학과 영어 성적의 상관관계

• 총 10명의 학생에 대하여, 수학과 영어 성적 예시

• 평균, 분산, 공분산을 계산

import matplotlib.pyplot as plt
X = [97, 85, 26, 54, 76, 15, 33, 83, 88, 91]
Y = [100, 92, 31, 61, 83, 28, 57, 45, 92, 93]
plt.plot(X, Y, 'o')
plt.xlabel("Math")
plt.ylabel("English")
plt.show()

x_mean = 0 # 평균(mean)
for x in X:
x_mean += x / len(X)
x_var = 0 # 분산(variance)
for x in X:
x_var += ((x - x_mean) ** 2) / (len(X) - 1)
print(f"x_mean = {x_mean:.3f}, x_var = {x_var:.3f}")
y_mean = 0 # 평균(mean)
for y in Y:
y_mean += y / len(Y)
y_var = 0 # 분산(variance)
for y in Y:
y_var += ((y - y_mean) ** 2) / (len(Y) - 1)
print(f"y_mean = {y_mean:.3f}, y_var = {y_var:.3f}")

import numpy as np
np.set_printoptions(precision=3)
import math
# 공분산(covariance)
covar = 0
for x, y in zip(X, Y):
covar += ((x - x_mean) * (y - y_mean)) / (len(X) - 1)
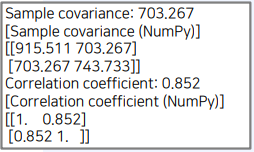
print(f"Sample covariance: {covar:.3f}")
print("[Sample covariance (NumPy)]")
print(np.cov(X, Y))
# 상관 계수(correlation coefficient)
correlation_coefficient = covar / math.sqrt(x_var * y_var)
print(f"Correlation coefficient: {correlation_coefficient:.3f}")
print("[Correlation coefficient (NumPy)]")
print(np.corrcoef(X, Y))

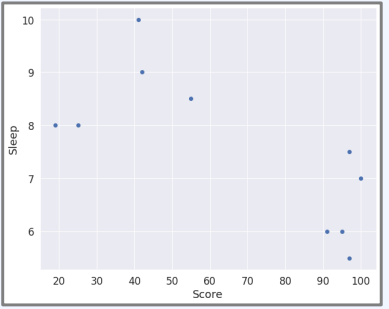
1. 두 데이터가 음의 상관관계를 가지는 경우

• 확률변수 X의 값이 크면, Y의 값은 작아지는 경우

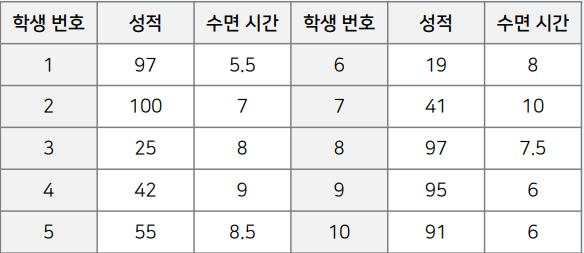
• 성적과 수면 시간 예시

import matplotlib.pyplot as plt
X = [97, 100, 25, 42, 55, 19, 41, 97, 95, 91]
Y = [5.5, 7, 8, 9, 8.5, 8, 10, 7.5, 6, 6]
plt.plot(X, Y, 'o')
plt.xlabel("Score")
plt.ylabel("Sleep")
plt.show()

x_mean = 0 # 평균(mean)
for x in X:
x_mean += x / len(X)
x_var = 0 # 분산(variance)
for x in X:
x_var += ((x - x_mean) ** 2) / (len(X) - 1)
print(f"x_mean = {x_mean:.3f}, x_var = {x_var:.3f}")
y_mean = 0 # 평균(mean)
for y in Y:
y_mean += y / len(Y)
y_var = 0 # 분산(variance)
for y in Y:
y_var += ((y - y_mean) ** 2) / (len(Y) - 1)
print(f"y_mean = {y_mean:.3f}, y_var = {y_var:.3f}")

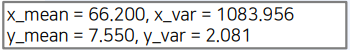
import numpy as np
np.set_printoptions(precision=3)
import math
# 공분산(covariance)
covar = 0
for x, y in zip(X, Y):
covar += ((x - x_mean) * (y - y_mean)) / (len(X) - 1)
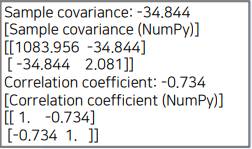
print(f"Sample covariance: {covar:.3f}")
print("[Sample covariance (NumPy)]")
print(np.cov(X, Y))
# 상관 계수(correlation coefficient)
correlation_coefficient = covar / math.sqrt(x_var * y_var)
print(f"Correlation coefficient: {correlation_coefficient:.3f}")
print("[Correlation coefficient (NumPy)]")
print(np.corrcoef(X, Y))