딥러닝을 위한 통계 Chapter 1-6 ( 13-17 )
딥러닝을 위한 통계 Chapter 1-6
1. 확률 분포의 추정
1-1. 확률 분포
- 우리가 가지고 있는 데이터로부터 확률 분포를 추정하는 기술
데이터의 형태를 보고 원하는 분포로 추정
- 베르누이 분포 : 데이터가 0 혹은 1의 형태
- 정규 분포 : 데이터가 크기 제한이 없는 실수 형태
- 카테고리 분포 : 데이터가 카테고리 값 형태
주어진 데이터를 이용해 확률 분포를 계산하는 방법
- 모멘트 방법
- 최대 가능도 추정
1-2. 모멘트
- 확률분포에서 계산한 특징 값의 일종
- n=1 : 평균
- n=2 : 분산
코드 예시
import math
arr = [1] * 3 + [2] * 5 + [3] * 7 + [4] * 10 + [5] * 6 + [6] * 6 + [7] * 3
mean = 0 # 평균
for x in arr:
mean += x / len(arr)
variance = 0 # 분산
for x in arr:
variance += ((x - mean) ** 2) / len(arr)
std = math.sqrt(variance) # 표준 편차
print(f"평균: {mean:.3f}")
print(f"분산: {variance:.3f}")
print(f"표준 편차: {std:.3f}")
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [10, 8]
x = np.linspace(mean - 10, mean + 10, 1000) # 평균(mean)을 중심으로 다수의 x 데이터 생성
# 정규 분포의 확률 밀도 함수(probability density function)
y = (1 / (np.sqrt(2 * np.pi) * std)) * np.exp(-1 / (2 * (std ** 2)) * ((x - mean) ** 2))
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel("$f_X(x)$")
plt.show()
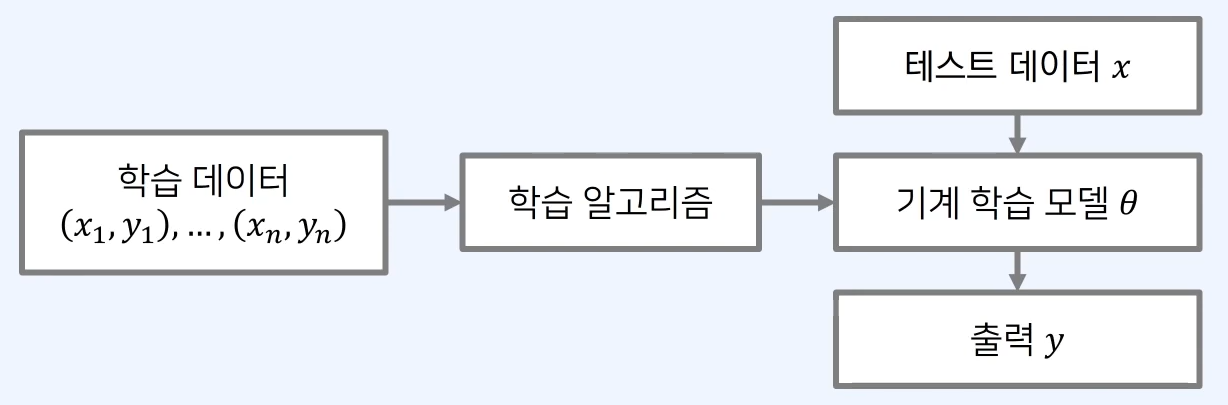
2. 최대 가능도 추정
2-1. 최대 가능도 추정
- 이론적으로 가장 가능성이 높은 parameter를 찾는 방법
- 가능도를 최대로 만드는 parameter를 찾는것
가능도 함수 : $L(\theta; x) = p(x; \theta) $
확률 분포에 따른 가능도 함수
- 베르누이 확률 분포
- $\theta = \mu$
- 정규 분포
-
$\theta = (\mu, \sigma^2)$
-
정규 분포의 평균은 표본 평균과 같고 분산은 표본 분산과 같음
3. 편향과 오차
3-1. 편향(Bias)
- 평향이 높을 때 : 모델이 예측한 값이 정답과 멀리 떨어져 있는 경우
- 분산이 높을 때 : 모델이 예측한 값이 서로 멀리 떨어져 있는 경우
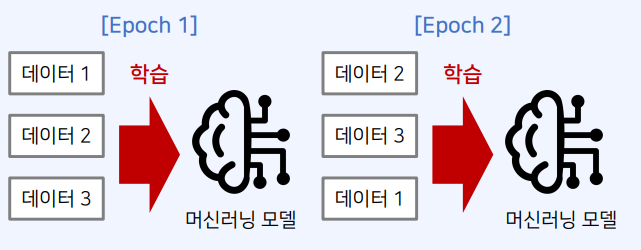
3-2. 오차(Error)
- 실제 정답과 우리 모델이 예측한 값의 차이
- 기계 학습 모델의 성능을 평가하기 위해 오차를 계산하는 과정이 필요
- 오차는 내 모델이 얼마나 잘못되었는지 알려주는 수치화된 값
- 비용(cost) 혹은 손실(loss)이라고도 부름
\[MSE = \frac{1}{N}\sum^N_{i=1}(f(x_i)-y_i)^2\]MSE
- 오차를 제곱한 값의 평균
- 입력 x, 정답 y
예시
$(f(x; \theta)-y)^2$
- y = 27로 가정
- x = 29 라면, 오차는 $(27-29)^2 = 4$
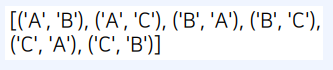
4. 최소 제곱법과 추세선
4-1. 선형 회귀
- 장사꾼의 매출 문제
Q. 7시간을 일 했을 때 매출은 얼마 일까?

-
입력(노동 시간)과 출력(매출)이 선형 함수(일차 함수) 형태를 가짐
-
선형 회귀: 주어진 데이터를 학습하여 가장 합리적인 선형 함수를 찾아내는 문제
-
아래 함수 중에서 데이터를 가장 잘 나타내는 선형 함수는 무엇인지 찾는 것
가설 함수 : $ f(x) = Wx+b$
선형 회귀에서 학습이란.
-
가장 합리적인 parameter( W와 b)를 도출하는 것
-
주어진 데이터를 이용해 선형 함수를 수정해 나가는 것
4-2. 비용(cost)
- 우리의 모델이 뱉은 답이 실제 정답과 얼마나 다른지 수치화 한 것
- 정확하지 않다면, 높은 값이 발생
- 다른 말로 손실(loss)라고도 함
최소 제곱법
- $(실제값 - 예상값)^2$의 합으로 비용을 계산
- m : 데이터의 개수 \(cost(W,b) = \frac{1}{m}\sum^m_{i=1}(H(x_i)-y_i)^2\)
4-3. 경사 하강
- 최소 제곱을 얻는 방법 중 하나
- 기울기를 이용하여 비용을 줄이는 방법
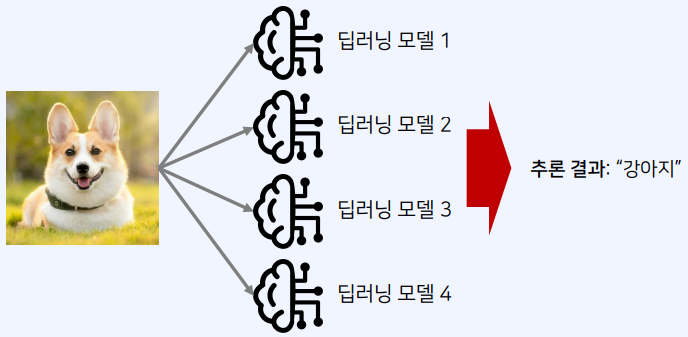
- 비용함수를 가중치(W)로 미분해 기울기를 구한 뒤 기울기의 반대 방향으로 W를 업데이트
5. 데이터 추출
5-1. 데이터 추출 (Data Sampling)

- 기계 학습 분야에서는 데이터를 랜덤으로 추출하는 경우가 많음
코드 예시
choice
import random
arr = [1, 2, 3, 4, 5]
sampled = random.choice(arr)
print(sampled)
# 1부터 5사이의 정수 중 하나
sample
import random
arr = [1, 2, 3, 4, 5]
sampled = random.sample(arr, 3)
print(sampled)
# 1부터 5사이의 정수 3개를 포함한 리스트
중복 허용
choice
import random
arr = [1, 2, 3, 4, 5]
sampled = [random.choice(arr) for i in range(3)]
print(sampled)
# 1부터 5 사이의 정수 3개를 포함한 리스트 (중복 가능)
𝑐ℎ𝑜𝑖𝑐𝑒𝑠()
import random
arr = [1, 2, 3, 4, 5]
sampled = random.choices(arr, k=3)
print(sampled)
# 1부터 5 사이의 정수 3개를 포함한 리스트 (중복 가능)
균등 분포
import numpy as np
sampled = np.random.uniform(0, 1, 5)
print(sampled)
# 0부터 1사이의 5개의 수
정규 분포
import numpy as np
sampled = np.random.normal(0, 1, 5)
print(sampled)
# 평균 : 0, 표준편차 : 1

Leave a comment