강화학습 Chapter 3. 벨만 방정식
개요
- 대부분의 강화학습 알고리즘은 Value를 구하는 것에서 출발
- 어떠한 상태를 평가 할 수 있어야 행동을 어떻게 교정 할 것인지 알수있음
- Value를 구하는 데 뼈대가 되는 수식이 바로 벨만 방정식
- 벨만 기대 방정식과 벨만 최적 방정식이라는 두 종류의 방정식을 배움
1. 벨만 기대 방정식
1-1. 벨만 기대 방정식 정의
- Value( $S_t$와 $S_{t+1}$)의 재귀적 관계에 대한 식
- 재귀적 관계란?
- $ X_{t-1}, X_t, X_{t+1} $ 등 사이의 관계
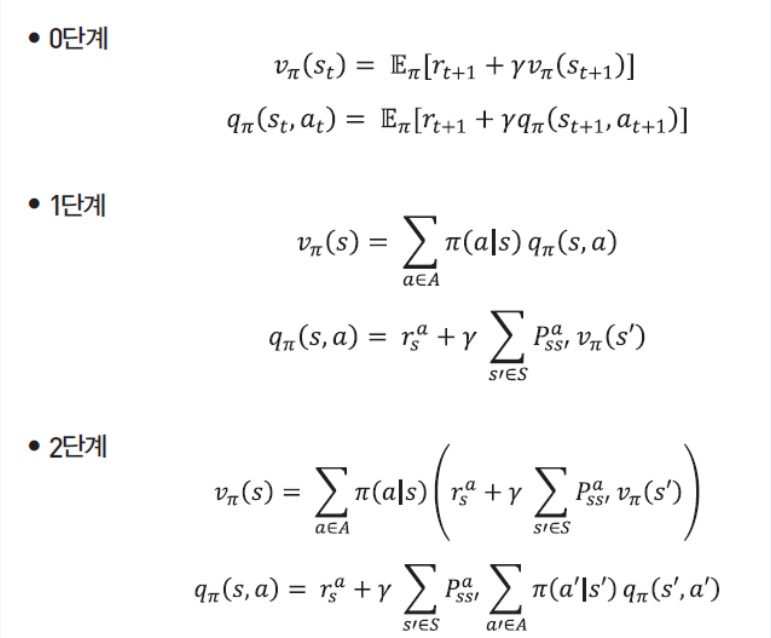
1-2. 0단계
- 수식
-
현재상태의 Value($ \upsilon_\pi(S_t) $)는 리워드($ r_{t+1} $)를 하나 받고 그 다음상태의 Value($ \gamma\upsilon_\pi(S_{t+1}) $)를 더한것과 같다 (무조건은 아님)
-
증명
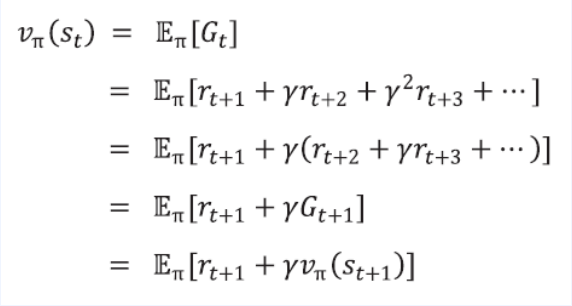
$ E[x] $ 기댓값이 들어간 이유
$ S_t $ 확률 변수는 사건마다 값이 달라지기 때문에 수식에 $ E[x] $ 기댓값이 포함됨
두 번의 동전 던지기
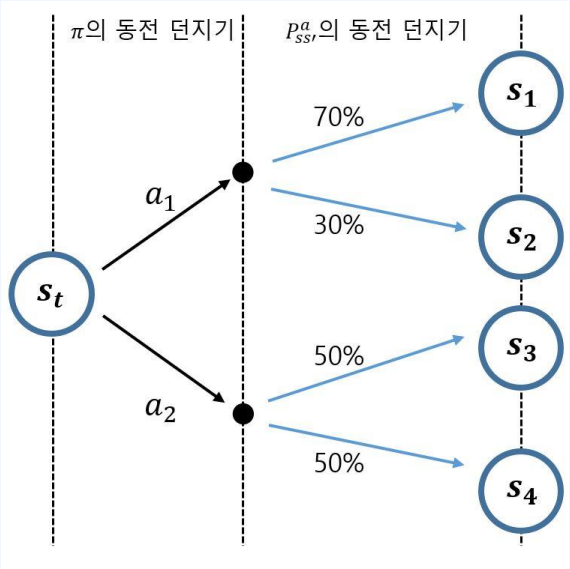
- $ S_t $에서 시작해 $ S_{t+1} $이 정해지기까지의 과정
- 총 두번의 확률적인 과정이 있다.
- $ \pi $의 동전 던지기 ( Policy )
- $ P^a_{ss`} $의 동전 던지기 ( 환경 )
- 0단계의 기댓값 연산자에는 이 두번의 과정이 포함되어 있다.
1-3. 1단계
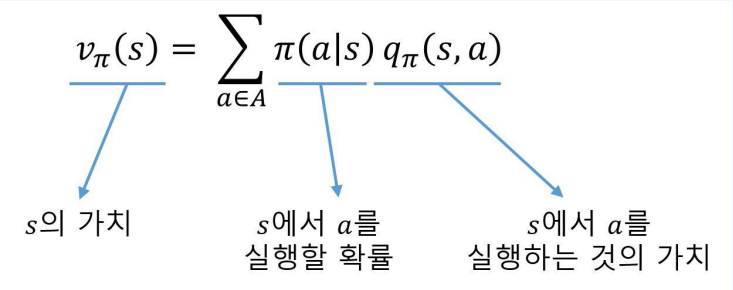
$ q_\pi $를 이용해 $ \upsilon_\pi $계산하기
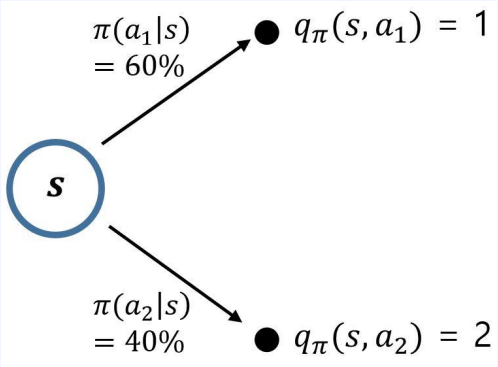
-
위와 같이 각 액션에 대한 $ q_\pi $의 값이 주어져 있을 때 상태 $s$의 밸류 $\upsilon_\pi(s) $를 구하고 싶다면?
-
위 수식을 이용해 현재 상태의 Value를 구한다면
-
$ 0.6 \times 1 + 0.4 \times 2$
$ \upsilon_\pi $를 이용해 $ q_\pi $계산하기
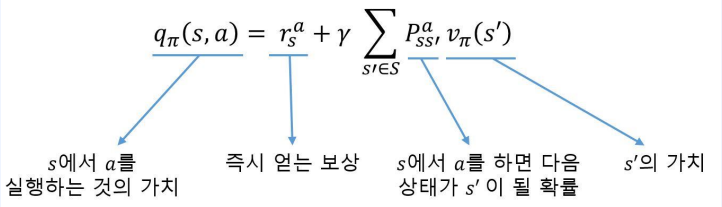
- 상태에서 액션을 하면 $ r^a_s $를 먼저 받는다.
- 어떠한 다음 상태에 도달할지 모르기 때문에 다음상태 $s’$의 가치와 $s’$가 될 확률을 곱하고 이를 다 더한 값을 더하면 된다.
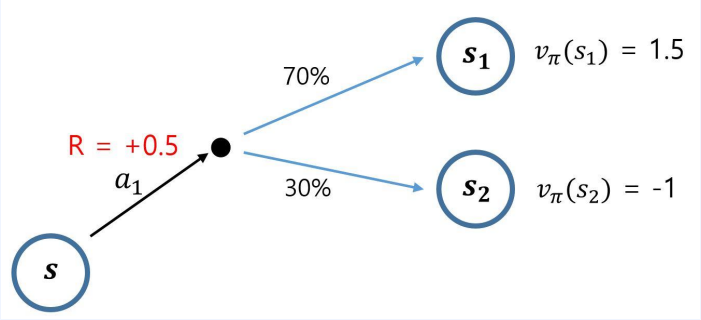
-
수식을 이용한다면
-
$ 0.5 + (0.7 \times 1.5 + 0.3 \times -1) $
1-4. 2단계
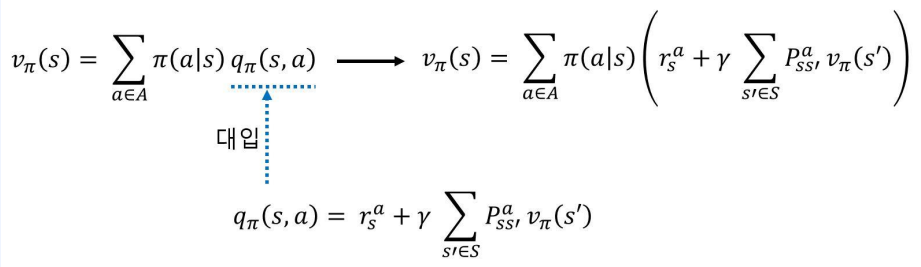
- 1단계 두 식을 조합하면 완성됨
1-5. 단계별 쓰임세
- 벨만 방정식은 Value를 구하는데 쓰임
- 0단계는 수식안에 전이 확률이 없음
- 2단계는 수식안에 전이 확률이 있음
- 따라서 MDP에 대한 정보를 모를 때는 0단계 ( Model Free)
- MDP에 대한 정보를 알 때는 2단계 ( Model Based )
- 이후 다시 공부 할 내용
2. 벨만 최적 방정식

-
벨만 기대 방정식에서 최대값이 추가 되었고 정책($\pi$)이 사라졌다
-
Optimal Value의 재귀적 관계에 대한 식
2-1. Optimal Value
- MDP가 주어졌다는 것은 상태, 액션, 전이확률, $\gamma$, 리워드가 고정 되었다는 것
-
어떤 MDP가 주어졌을 때, 그 MDP 안에 존재하는 모든 $\pi$들 중 가장 좋은 $\pi^* $를 선택하여 계산한 상태 $s$의 Value($v_*(s)$
-
가장 좋은 $\pi^*$란? 비교를 하기 위해서 더 좋은이나 더 나쁜것이 먼저 정의해야 한다.
- 무엇이 더 좋은지 정의 할 수 있는 경우
- 모든 상태 $s$에 대해 $v_{\pi_1}(s) >= v_{\pi_2}(s) $
Optimal Politcy
- 다음과 같이 증명된 정리가 있음
- 모든 MDP에는 $\pi^*$가 존재한다.
- $\pi^* $는 MDP 안에 존재하는 모든 $\pi$에 대해 $\pi^* >= \pi$를 성립

2-2. 0단계
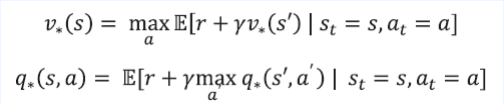
- a에 따라서 값은 달라진다.
- 한 스텝 진행하고 나서 $s’$의 옵티멀 밸류를 사용하여 $s$ 옵티멀 밸류를 max로 묶은것
2-3. 1단계
$ q_* $를 이용해 $ \upsilon_* $계산하기

$ \upsilon_* $를 이용해 $ q_* $계산하기
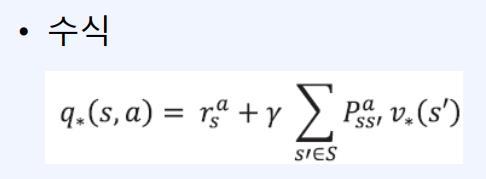
- $s$에서 $a$를 선택했을 때의 Optiaml value는 $a$를 선택했을 때의 리워드를 받고 다음에 도달하게 되는 상태들의 optimal value와 그 상태에 도달할 확률의 곱
2-4. 2단계

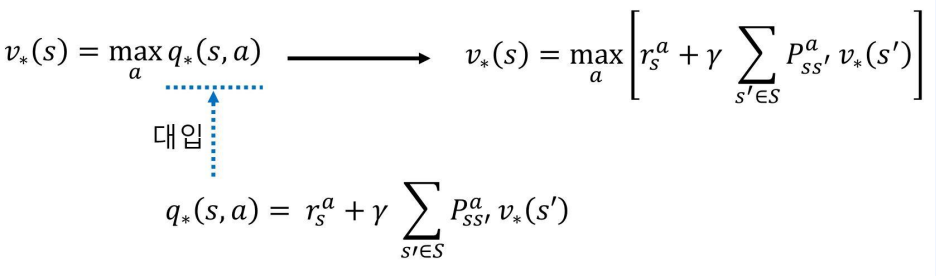
- 마찬가지로 1단계 두 식을 조합해서 만듬
1-5. 단계별 쓰임세
- 벨만 방정식은 Value를 구하는데 쓰임
- 0단계는 수식안에 전이 확률이 없음
- 2단계는 수식안에 전이 확률이 있음
- 따라서 MDP에 대한 정보를 모를 때는 0단계 ( Model Free)
- MDP에 대한 정보를 알 때는 2단계 ( Model Based )
- 이후 다시 공부 할 내용

Leave a comment