강화학습 Chapter 4. MDP를 알 때의 플래닝

개요

• 앞서 벨만 방정식을 배운 덕분에 이제는 실제로 간단한 MDP를 풀 수 있습니다.
• 벨만 방정식을 반복적으로 적용하는 방법론을 통해 아주 간단한 MDP를 직접 풀어봅니다.

1. Value 평가하기

• 작은문제
  • 작다는 것은 다음의 가짓수가 작은 것을 의미
    • Action space
    • State space
    • Time horizon
• MDP를 알 때
  • $ MDP \equiv {S, A, R, P, \gamma } $
  • $ R, P$ 를 알 때
    • 여기서 안다는 것은 해보기도 전에 미리 아는 것

1-1. 문제 설정

술취한 사람의 귀가 문제 ( 그리드 월드 )

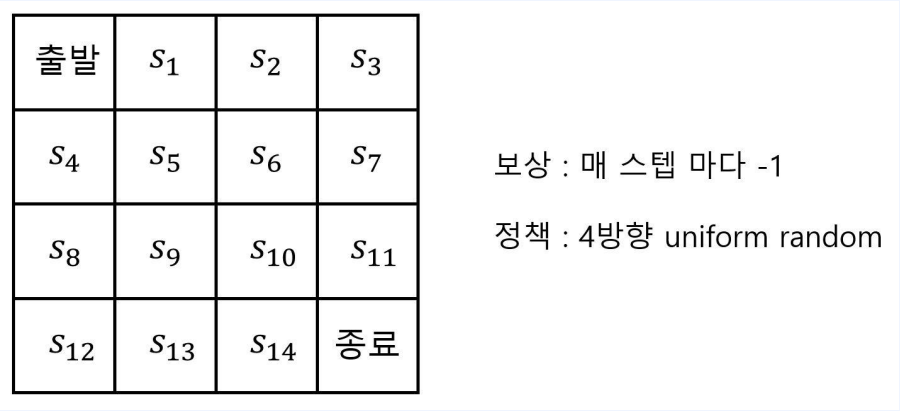
• 이때 각 state의 Value는?
  • 평균적으로 종료까지 몇 칸이 걸리냐와 같은 뜻
• 위 문제의 정보를 종합하면
  • Policy가 주어졌을때 state들의 Value func을 구하고자 한다.
  • state = 16, action = 4, reward = -1, 다음 상태(전이확률)도 예측 가능
• 다음 방법론으로 풀어보자

1-2. Iterative Policy Evaluation

• 반복적으로 주어진 정책을 평가하는 것

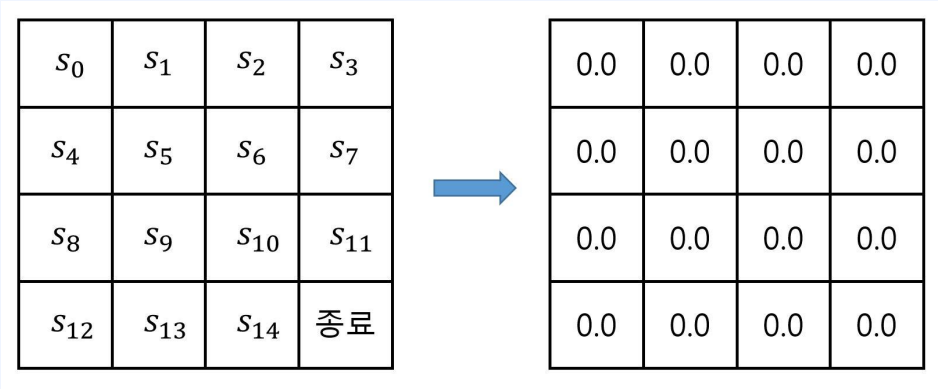
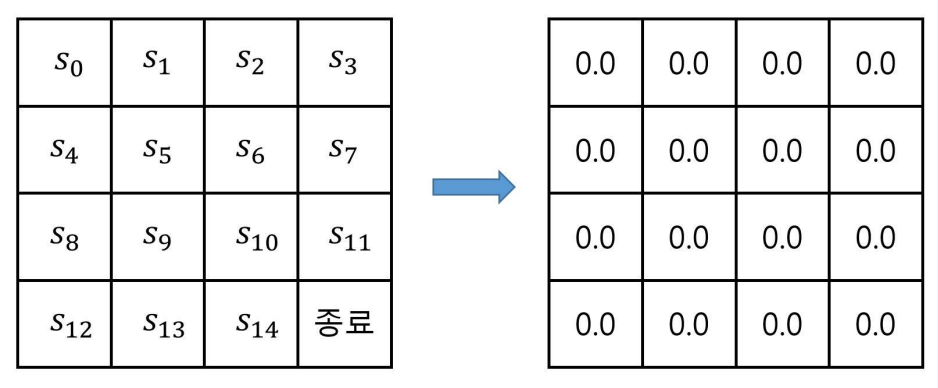
• 각 상태마다 값을 적어놓을 테이블을 만든다.
• 이 테이블의 값을 임의의 값으로 초기화 한다.

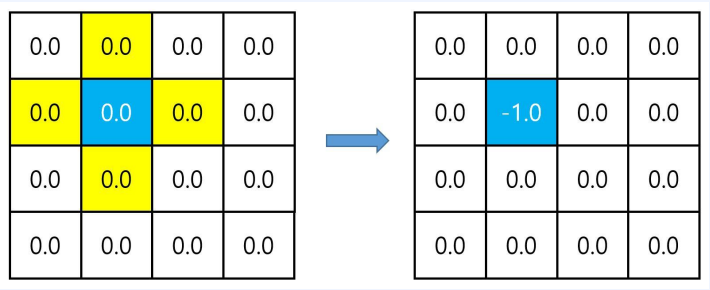
• 벨만 기대방정식을 이용해 파란색 상태의 값을 업데이트 할 계획
• 벨만 기대방정식 2단계 이용
  • 리워드와 전이확률을 알기 때문

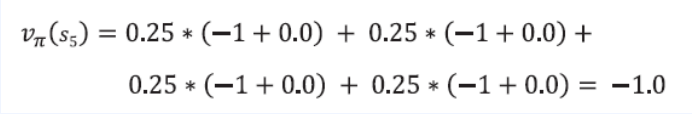
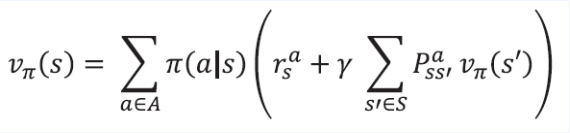
• $\pi(a \mid s) = 0.25 $
• $r^a_s = -1$
• $\gamma = 1$
• $\sum_{s’ \in S}P^a_{ss’} = 1$ ( 모든 위치들의 합 )
• $v_\pi(s’) = 0$ ( 노란색 )

업데이트 된 값이 더 나은 값인지 확인해보자

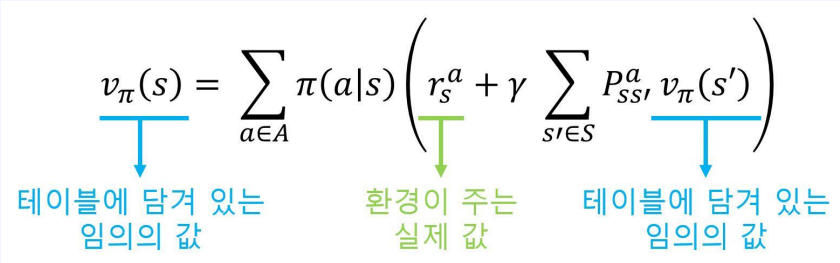
• 환경이 주는 실제 값은 정답이다
• 따라서 처음엔 임의의 값이었지만 조금씩 조금씩 정확한 값으로 바뀌어 간다

---

환경이 주는 실제 값이 정답인 이유

• 종료지점은 0으로 고정된다 즉 정답이다

• 예를 들어 벨만 방정식은 재귀적 관계이므로 $s_{10}$은 $s_{11}$의 값으로 유추 가능하다. 그렇다면 $s_{11}$은 종료지점과 연관이 생기므로 모든 상태($s$)는 종료지점과 연관이 있다.
• 이러한 벨만 방정식을 사용하여 업데이트 된 값은 더 나은 값이 될 것이다.

---

• 계속 반복하게 되면 정답에 수렴할 것이다.

2. 최적 정책 찾기

2-1. Policy Iteration

• 크게 두단계로 나뉘는데 그중에서 Policy improvement를 먼저 알아보자.

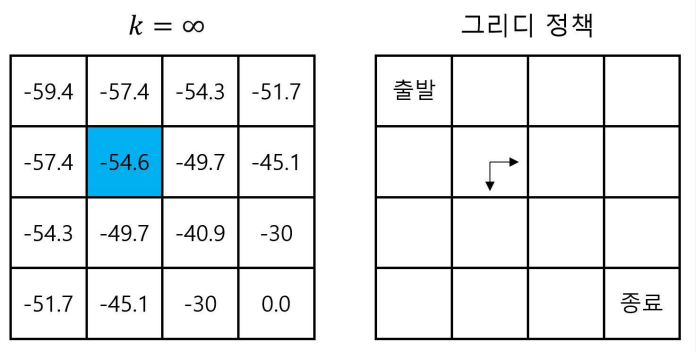
• 먼저 파트 1에서 구한 Value 테이블을 가져옵니다.
• 여기서 괴상한 정책 $\pi’$를 생각해봅시다.
  • 일단 무조건 Value가 높은곳으로 한칸 움직이고 그 다음은 기존 $\Pi$(4방향 랜던 정책)으로 움직인다.
• 이렇게 하면 $\pi’$은 $\pi$보다 더 나은가?

• 위 그림의 파란색으로 표기된 -54.6의 Value를 지닌 칸에서 시작합니다.
  • $\pi$를 따라서 끝까지 움직일때의 가치가 -54.6 입니다.
• 하지만 앞선 새로운 괴상한 정책 $\pi’$으로 움직이게 된다면
  • 먼저 Value가 높은 곳으로 한칸 움직인다면 reward로 인해서 -1을 얻을 것이고 -49.7의 Value를 가진곳으로 이동합니다.
  • 다음으로 $\pi$를 따라서 끝까지 움직일때의 가치는 -49.7 + (-1)이 됩니다.
• 그러므로 $\pi$ = -54.6의 가치를 가지는 반면 $\pi’$은 -50.7의 가치를 가지고 모든 상태에서 만족하기 때문에 $\pi’$은 $\pi$보다 더 나은 정책이라 할 수 있습니다.

만약 같은 논리를 $\pi’$에도 적용한다면? 그리고 그것을 계속 반복 한다면?

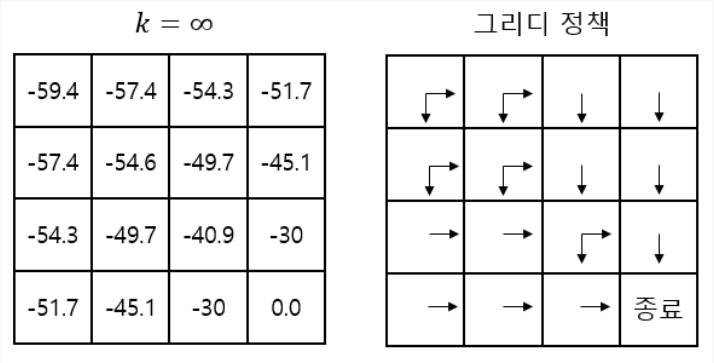
• 위와 같은 Greedy Policy가 생성된다.
• 기존 정책 $\pi$보다 개선된, 더 나은 정책을 찾았다.
• 즉 Policy improvement(정책 개선)가 이루어 졌다. ___

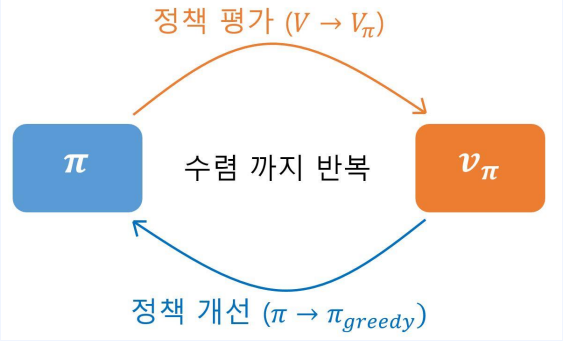
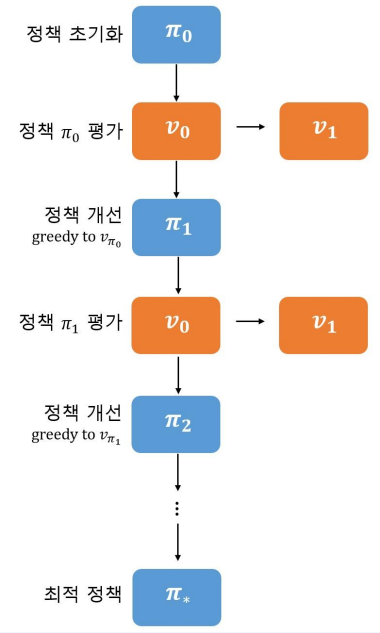
• 정책 평가 ( Policy evaluation ) -> iterative policy evaluation

• 정책 개선 ( Policy improvement ) -> greedy policy

• 이둘을 계속해서 반복하면 더 나은 정책이 생성된다. 좀 더 자세한 그림은 아래와 같다.

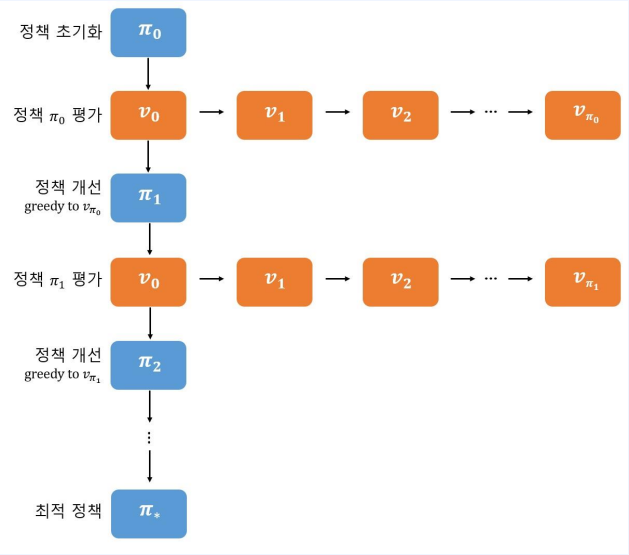
• 이 구조를 보게 되면 Policy Iteration의 반복되는 구조 안에 Policy evaluation의 반복 구조가 있다. 즉 평가 부분에서 연산이 많다는 의미입니다.

그렇다면 평가 부분을 줄일 수 없을까?

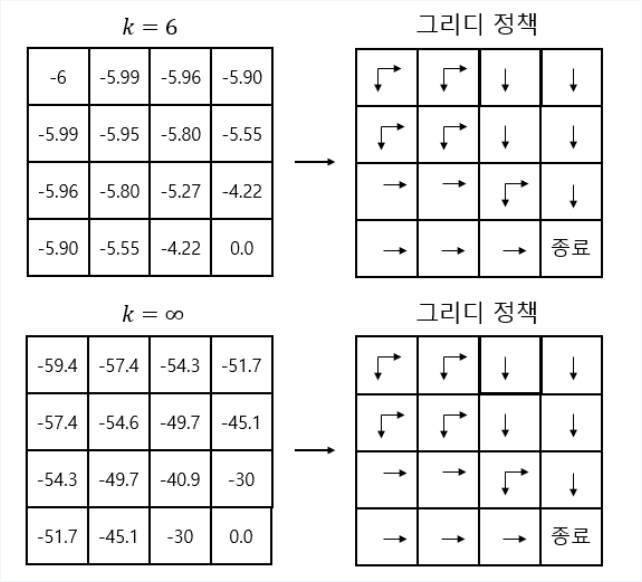
• Policy evaluation 과정중 6번째와 무한번째의 Greedy policy는 동일하다.
• 즉 꼭 수렴할 때 까지 돌릴 필요가 없다는 것을 보여준다.
• 다음과 같이 간소화 할 수 있다.

• 이렇게 해도 최적 정책으로 수렴함이 알려져 있습니다.

2-2. Value Iteration

• 앞서 Policy Iteration은 평가와 개선의 반복이었고 벨만 기대 방정식을 사용하여 구하였습니다.

• Value Iteration은 평가와 개선과 같은 중간 과정없이 Optimal value를 구하고자 하는 것입니다.

• Optimal policy는 Optimal Value를 가지고 있고 3파트에서는 Optimal value($v^*(s)$)를 구하는것에 대해서 알아보고자 한다.

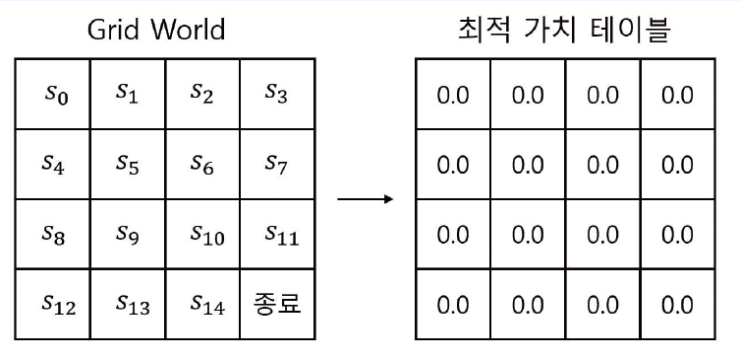
• 각 상태별 Optimal Value를 저장하기 위한 테이블
• 초기화 값은 어떤 값이어도 상관없습니다.

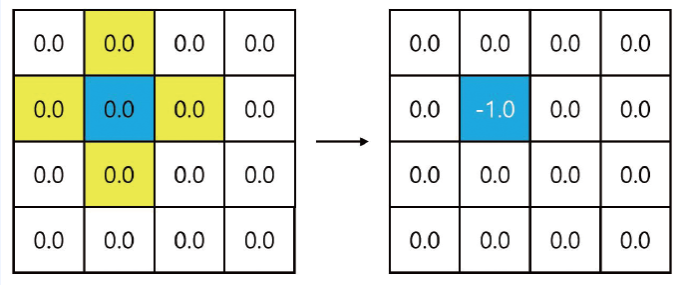
• 벨만 최적방정식 2단계 수식을 적용

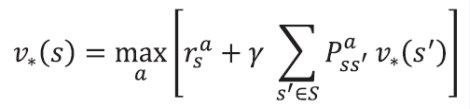
• $r^a_s = -1$
• $\gamma = 1$
• $\sum_{s’ \in S}P^a_{ss’} = 1$ ( 모든 위치들의 합 )
• $v_\pi(s’) = 0$ ( 노란색 )

$ \begin{matrix} v_*(s_5) = max(-1 + 1.0 * 0,\ -1 + 1.0 * 0, \ \qquad\qquad\qquad\ \ \ -1 + 1.0 * 0, \ -1 + 1.0 * 0,)\ = -1.0 \end{matrix}$

• 2파트와 같이 모든 값을 업데이트 합니다.

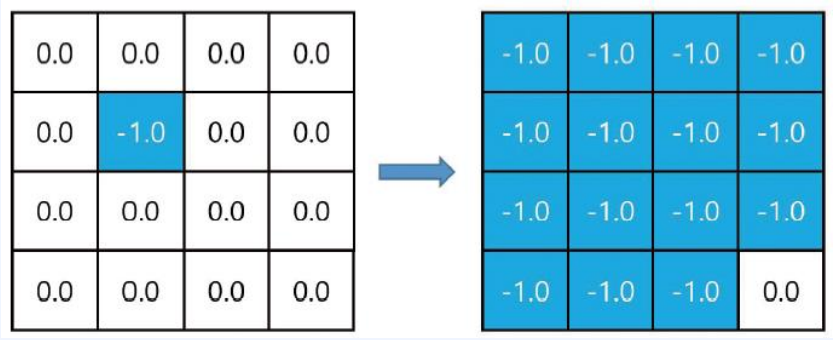
• 여러번 업데이트 한다면 다음과 같이 될 것입니다.

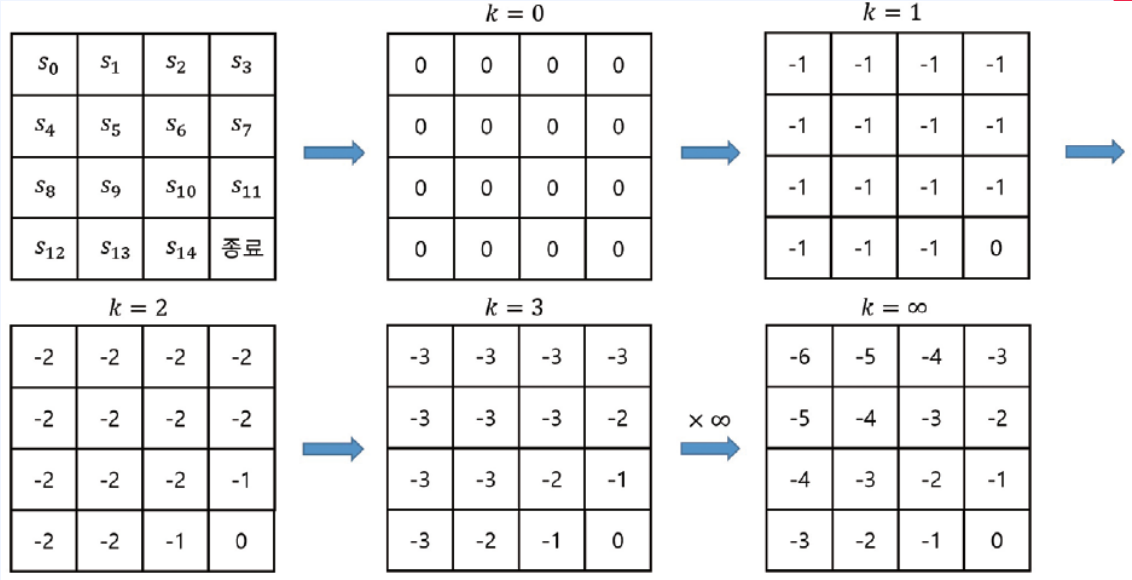
• Optimal Value(최적 밸류)는 얻었다. 그렇다면 최종 Policy는 어떻게 얻어야 하나?
  • 각 상태별 취할 수 있는 액션 중 다음 상태가 가장 좋은 것을 고르면 된다.
  • 다시 말해 다음 상태의 최적밸류 기댓값이 가장 높은 액션을 고른다.