강화학습 Chapter 5. MDP를 모를 때의 밸류 평가

개요

• MDP의 전이 확률($P$)와 보상 함수($R$)를 모를 때를 가정합니다.
• 주어진 수식을 이용해 정확한 값을 계산하는 대신, 수많은 샘플을 통해 근사하는 샘플 기반 방법론이 도입

1. Monte Carlo Learning ( MC )

동전의 기댓값을 알고 싶다면?

• 그냥 여러 번 던져보면 된다.
• 여러 번 던질 수록 대수의 법칙에 의해 실제 기댓값으로 수렴
• 이러한 샘플링 기반 추정 방법론을 Monte Carlo 방법론이라 부른다.
• 밸류의 정의 -> $v_\pi(s) = E_\pi[G_t]$

1-1. Monte Carlo Learning

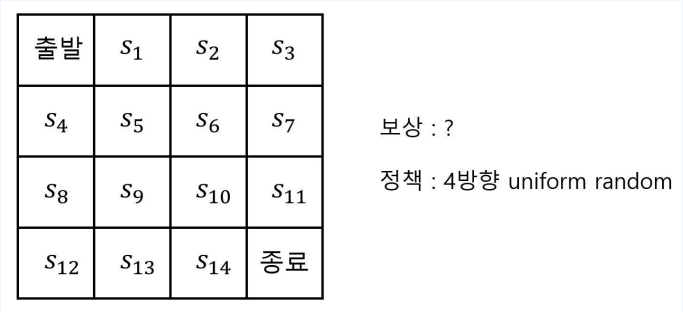
• 저번 챕터의 술 취한 행인 문제 입니다.
• 이번에는 $r^a_s, p^a_{ss’}$을 모르는 상황
• MC를 적용해서 Value를 구하고 싶다.

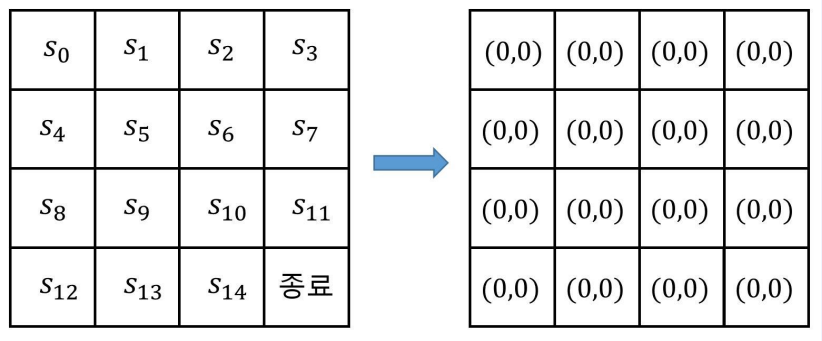
• 문제가 작기 때문에 여전히 테이블 기반 방법론을 사용
• 임의의 값으로 초기화
• 임의의 값은 (방문횟수, 리턴)로 무수히 반복해서 경험을 쌓을 예정

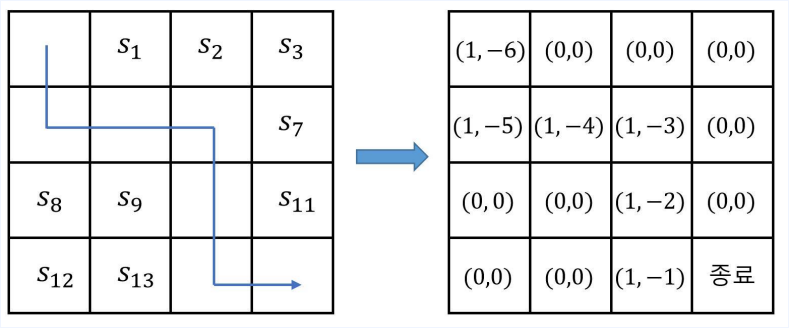
• 경험을 쌓는 과정
• 파란 선과 같은 경로를 따라서 종료에 도달했다고 가정
• 방문횟수 $ N(s_t) \leftarrow N(s_t) + 1$
• 리턴 $ V(s_t) \leftarrow V(s_t) + G_t$
• Value $ v_\pi(s_t) \cong \frac{V(s_t)}{N(s_t)}$

조금씩 업데이트 하는 버전

• 원래 식은 에피스드 n개가 다 끝난 후에 평균을 냈다.
• 이번에는 에피소드가 1개 끝날 때마다 테이블을 업데이트 하는 버전
• $\alpha $는 얼만큼 업데이트 할지 정해주는 파라미터 ( learning late )
• 다음과 같이 표현 가능 \(V(s_t) \leftarrow V(s_t) + \alpha(G_t - V(s_t))\)

2. Temporal Difference Learning

MC의 단점

• 바로 업데이트를 하려면 에피소드가 끝날 때 까지 기다려야 한다는 것
• 리턴은 에피소드가 끝나야 결정되는 값

---

• 그렇다면 에피소드가 끝나지 않은 상태에서 스텝마다 업데이트할 수는 없을까?

2-1. 추측으로 추측을 업데이트 하는 아이디어

• 오늘은 금요일이다. 그리고 일요일에 비가 내릴지 맞히고 싶은 상황
• 비가 올지 정확히 추측하는 것은 $ 일요일 > 토요일 > 금요일 $ 순으로 가능하다.
• 그렇다면 토요일에 추측한 내용을 조금 더 나은 값으로 보고 금요일의 추측을 업데이트 할 수 있지 않을까?

2-2. TD

이론적 배경

• MC를 쓸 수 있었던 이유
  • $G_t$를 여러 번 뽑아서, 이를 평균 낼 수 있었던 이유
  • $v_\pi(s_t) = E_\pi[G_t]$ 이기 때문
  • Value가 평균의 기댓값이기 때문
• 벨만 기대 방정식 0단계를 떠올려보자
  • $v_\pi(s_t) = E_\pi[r_{r+1} + \gamma v_\pi(s_{t+1})]$
  • $r_{t+1} + \gamma v_\pi(s_{t+1})$를 여러 번 뽑아서 평균내도 된다는 뜻

---

TD Learning 알고리즘

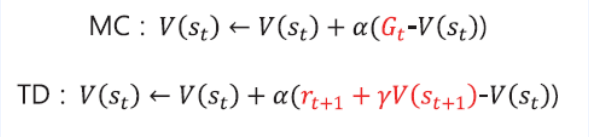
• MC에서 “조금씩 업데이트 하는 버전”에 해당하는 식
• MC에서 정답지 자리에 들어갔던 $G_t$
• 그 자리에 대신 $r_{t+1} + \gamma V(s_{t+1})$이 들어갔다.
• $v_\pi$와 $V$는 다르다. 달라도 됩니다. ( 이유는 나중에 설명 )

---

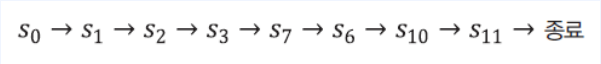
• 다음과 같은 상태를 방문하고 에피소드가 종료됐다고 가정
• 각 상태의 Value는 다음과 같이 업데이트 됨

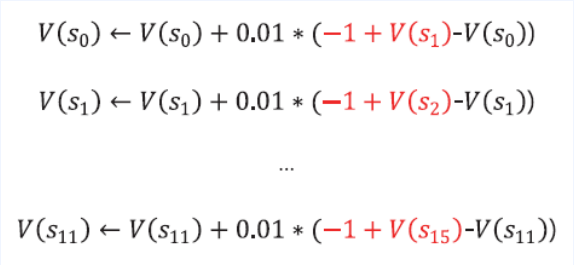
3. MC vs TD

3-1. 같은 일을 하는 두 옵션

• MDP의 $r^a_s, p^a_{ss’}$를 모르는 상황
• 직접 해보고 값을 찾아야 한다
• 그래서 두가지를 3가지 평가 지표에 의해 비교해 보고자 한다.

3-2. 학습 시점

• MC는 에피소드가 끝나야 가능
• TD는 한 스텝만 끝나도 바로 학습 가능
• 따라서 TD가 더 유연하게 사용 가능

3-3. Bias

• 먼저 MC와 TD의 수식을 살펴보자

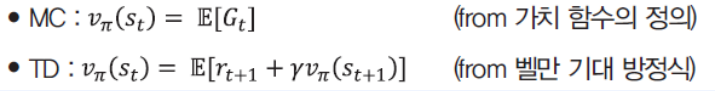
• MC는 리턴($G_t$)을 사용한다. Value를 구하는데 있어서 편향되지 않은 추정치를 나타낸다.
  • 리턴을 모두 다 더하게 되면 정답에 가까워 질 것이기 때문
• TD를 편향되지 않게 만들려면 $v_\pi$를 계산 해야함
  • $v_\pi$는 알 수가 없다.
  • 그래서 테이블 안에 있는 값($V(s)$)을 사용

3-4. Variance

Variance란?

• 정답이 500이라고 가정
• 1번 머신 : 0~1000 사이 숫자가 랜덤하게 나옴
• 2번 머신 : 501~503 사이 숫자가 랜던하게 나옴

• 어느 머신을 학습하는게 더 나을까?

• 쉽게 생각해서 n번 뽑는다고 생각하자. 그러면 각 머신 별로 평균치가 나올 것이다.
• 1번 머신은 n이 낮으면 평균이 500과 차이가 많이 날 것이고
• 2번 머신은 n이 낮아도 평균이 500과 최대 3차이가 날 것이다.
• 실제로는 무한정 학습하지 않는다.

• 따라서 2번 머신이 더 나은 것을 확인할 수 있다.

• MC에서 사용되는 리턴은 한 개의 값을 얻기 까지 수많은 확률적 과정을 거친다.
  • 에피소드가 하나 끝나야 하기 때문
  • 한 스텝 사이에 2개의 확률적 과정
  • 한 에피소드에는 n개의 스텝

• 반면 TD는 한 스텝의 확률적 과정만 거치면 얻어짐

• 즉, 수많은 확률적 과정을 거치면 Variance는 커진다.
  • 예를 들어 서울에서 부산까지 차를 타고 가는길과 집앞의 편의점을 가는 길의 차이를 생각 하면 쉽다.

3-5. MC와 TD의 중간

• TD 타겟을 생각해보자
  • $ r_{r+1} + \gamma v_\pi(s_{t+1}) $
  • 이를 1스텝 TD라고 부른다.
• 자연스럽게 N스텝에 대해 생각을 해보자.

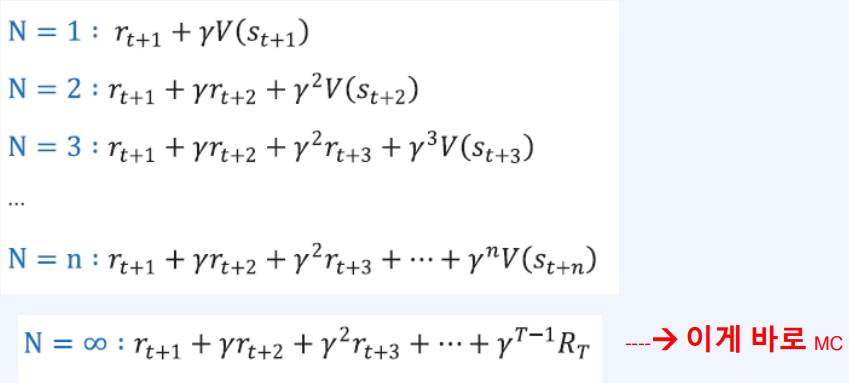
• 사실 MC와 TD는 전혀 다른 것이 아니다.

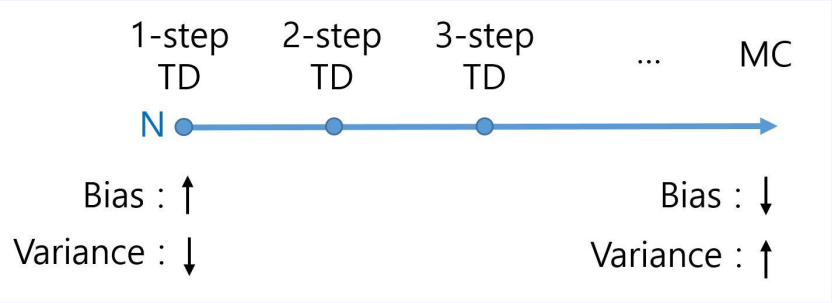
• 위 그림과 같이 TD에서 시작해서 MC로 끝나는 스펙트럼이 존재한다.
• 이 스펙트럼 가운데 Sweet spot을 찾아야 한다.
• 이는 학습하기 전까지 모른다.