MinUkiki

강화학습 Chapter 6. Deep RL 첫걸음

개요

  • 지금까지 작은 문제로 기초를 다졌다면 이제 큰 문제로 넘어갑니다.
  • 큰 문제로 넘어가면서 딥러닝이 필요해 집니다.

1. 함수를 활용한 근사

1-1. 근사는 왜 필요한가?

  • 체스와 바둑의 고유한 상태의 수를 세어보면?
    • 체스 : $10^{47}$
    • 바둑 : $10^{170}$
  • 테이블 기반 방법론을 적용하면 테이블의 크기도 클뿐만 아니라 필요한 시간이 너무 많이 소요된다.
  • 체스나 바둑보다 더 많은 state가 있는 자율주행하는 차에서 현재 속도가 state로 쓰인다면 state는 연속적이기 때문에 갯수는 무한에 가까울 것이다.

1-2. 함수의 등장

$f(x) = ax + b$

  • 앞서 테이블에 $s$와 $v(s)$ 또는 $q(s,a)$의 값을 넣었습니다.
  • 테이블에 값을 적어넣는 것이 아니라 함수에 값을 넣을 예정

예시

  • 속도가 100km/h 인 상태 $s_0$의 Value는 1
  • 속도가 200km/h 인 상태 $s_1$의 Value는 -10
  • (100,1), (200,-10)을 위 식에 대입
  • $f(s_0) = f(100) = 1$
  • $f(s_1) = f(200) = -10$
  • $a = 0.11, b = 12$
  • 하지만 값이 2개가 아니라 30개가 된다면?

img

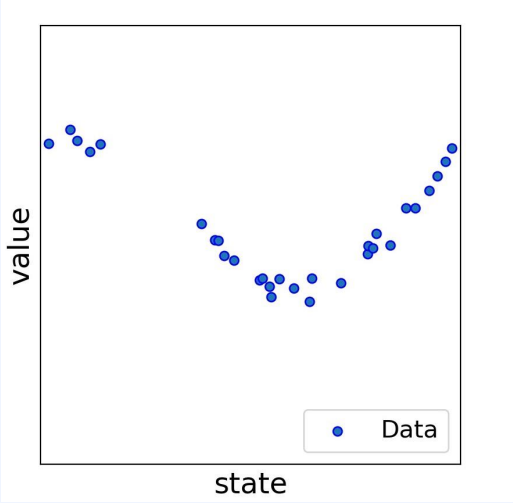
  • 30개를 지나는 a,b는 존재하지 않다. 하지만 그나마 가깝게 지나는 a,b는 찾을 수 있다.
  • 30개의 점은 (state, value)이며, 가깝게 지나는 것을 정의하면 다음 식(오차의 제곱의 합)을 최소화 하는 a,b를 구하는 것이다.

img

img

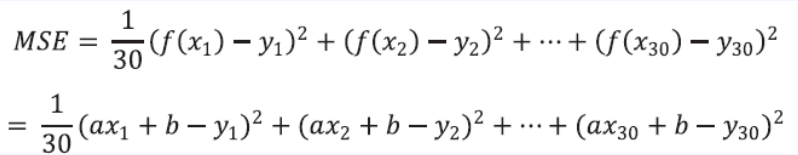
  • 최소화 되는 a,b를 찾으면 다음과 같은 빨간 선이 그어짐
  • 이런 과정을 fitting이라 부릅니다.
  • 피팅을 잘하기 위해서는 함수가 가지고 있는 파라미터들을 수정해야 합니다.
  • 하지만 꼭 일차함수 형태일 필요는 없다. 1차부터 n차 까지 다항 함수를 사용할 수 있습니다.

1-3. 함수의 복잡도에 따른 차이

  • 다시 한번 fitting에 대해 정리하면
    • 함수에 데이터를 기록
    • 데이터 점들을 가장 가깝세 지나도록 함수를 그림
    • 함수 $f$의 파라미터 ($a_0 \sim a_n$)의 값을 찾음
    • 함수 $f$를 학습

img

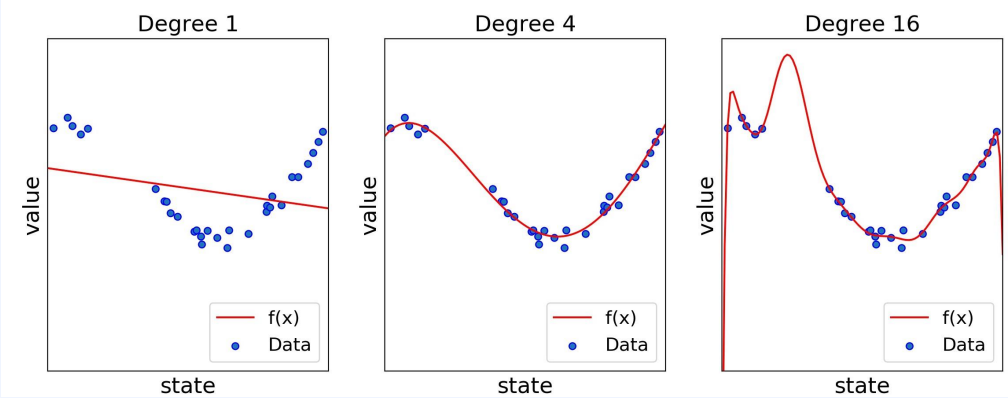
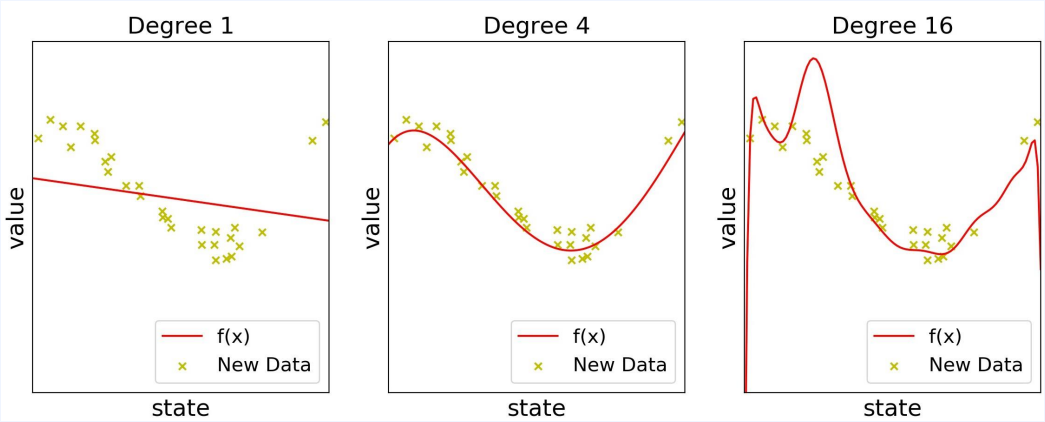
  • 각각 1차, 4차, 16차 함수로 학습한 결과입니다.
  • 더 유연한 함수를 사용할수록 주어진 데이터를 더 가깝게 지나느 선을 그릴 수 있습니다.
  • 데이터에 더 가깝게 지난다는 것은 에러가 줄어든다는 뜻
  • 각 경우의 MSE를 계산하면 0.3, 0.03, 0.00000002가 나옵니다.

차수가 높을 수록 좋은가?

  • 그렇지 않습니다.
  • 데이터에는 노이즈가 섞여 있기 때문

1-4. 함수의 장점

  • 왜 함수를 사용하면 저장공간이 덜 필요하나?
    • 접하지 않은 경우까지 정답을 알 수 있기 때문 ( 일반화 )

img

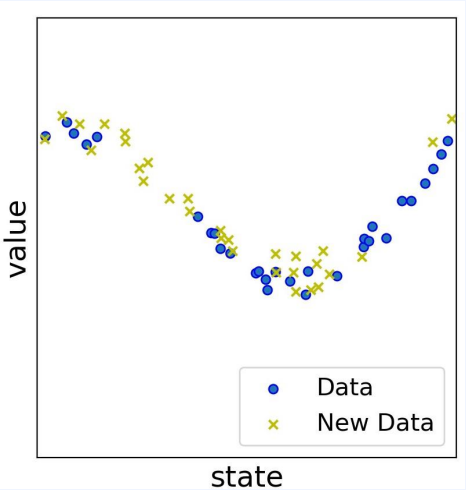
  • 파란점 : 30개의 데이터
  • 노란점 : 아직 경험 못한 새로운 30개의 데이터
  • 파란점에 대해 fitting 한다면?

img

  • 노란 점에 대해 잘 맞히는 경우도 있고 못 맞히는 경우도 있다.

2. 인공 신경망의 도입

  • 너무나도 유연해서, 세상의 어떤 복잡한 관계에도 fitting 가능
  • 유연성을 결정하는 숫자는 “프리 파라미터”의 개수

img

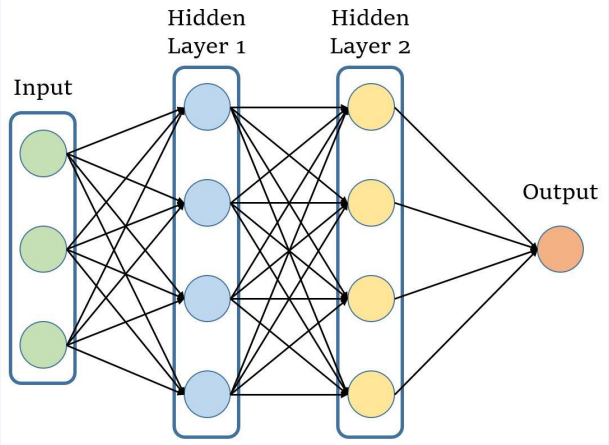
  • 길이가 3인 벡터를 인풋으로 받아 값 한개를 리턴하는 함수
  • $ y= f(x_1,x_2,x_3) $
  • 히든 레이어가 두층 쌓여 있다.
  • 각 히든 레이어는 여러 개의 노드로 구성되어 있다.

2-1. 노드의 연산

img

  • 각 노드는 해당 노드로 들어오는 값에 다음 두 과정을 적용함
    • 선형 결함(linear combination)
    • 비선형 함수(non-linear activation)
  • 선형 결합 : 파라미터 $ w, x, b $들의 연산 ( $w_1x_1 + w_2x_2 + w_3x_3 + b$ )
  • 비선형 함수 : $g(x)$ ( 여기서는 RELU ( $g(x) = max(0,x)$ )

2-2. 레이어에 따른 추상화

  • 선형 결합은 새로운 feature를 만드는 과정입니다.
  • 체스를 두는 에이전트를 학습한다고 가정
  • 현재 상태 벡터 s가 ( 룩의 수, 폰의 수, 비숍의 수 )로 표현된다고 가정
  • 총 말의 개수 자체가 중요하다면
    • $w_1 = w_2 = w_3 = 1$로 학습
    • “살아 있는 말의 수” 라는 추상화된 feature가 학습 된 것임

2-3. 그라디언트 디센트

img

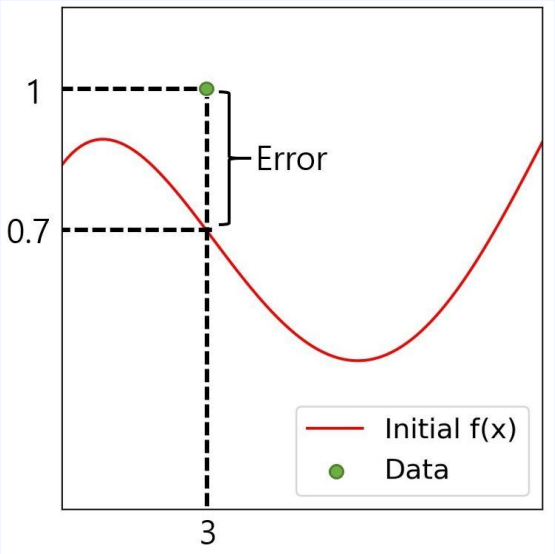
  • 손실함수
    • 정답이 주어졌을 때, 현재 뉴럴넷이 틀린 정도를 나타냄
    • $ L(w) = { 1-f_w(3)}^2$
  • 이 값을 줄이도록 파라미터 w를 수정하는 게 목표
    • 각 파라미터의 영향력을 구한다.

영향력이란?

  • $w$를 0.1만큼 증가시키면 함수 $L(w)$의 값이 0.1만큼 증가하더라
  • $w$를 0.1만큼 감소시키면 함수 $L(w)$의 값이 0.7만큼 감소하더라
  • 이를 식으로 표현하면
  • $\frac{\partial L(w)}{\partial w_1}$ ( 편미분 )
  • 모든 파라미터에 대해 모아주면 다음과 같은 벡터가 된다.

img

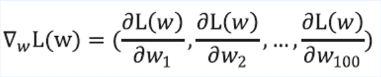
  • 이것을 gradient라고 부름
  • $w$를 gradient 방향으로 조금 이동 시켜주면 됩니다. 이를 수식화 하면 다음과 같다.

img

  • $\alpha$ = learning rate

이를 한줄로 표현 하면

\[W' = w - \alpha*\triangledown_w L(w)\]

간단한 확인

  • 다음과 같은 함수가 있다.
\[f_w(x_1, x_2) = w_1x_1 - w_2x_2 + 1\]
  • 파라미터 $w_1, w_2$는 랜덤한 값으로 초기화 되어 있음
    • $w_1 = 0.5, w_2 = 1.2$라 가정
  • fitting할 데이터 1개가 주어짐
    • $(x_1,x_2,y) = (1,2,1)$
    • 현재 $f_w(1,2) = -0.9$ ( $f_w(x_1, x_2) = y$ )
    • 이를 loss func로 정의

img

  • 이를 이용해 gradient를 구해보면

img

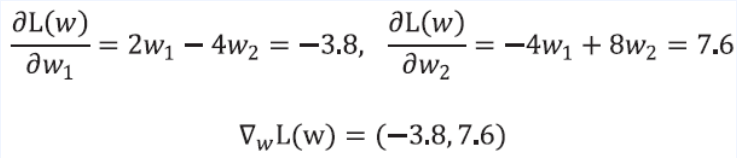
  • 이를 이용해 파라미터를 업데이트 해보면

img

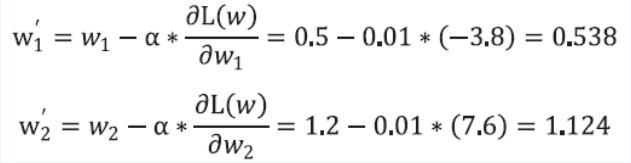
  • 업데이트 되고 정말 값이 1 정답에 가까워진 것을 확인할 수 있다.

img

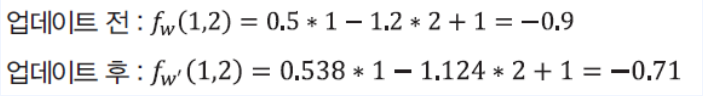
3. Pytorch로 인공 신경망 실습

3-1. 문제 세팅

  • 학습하고자 하는 함수
    • input과 output은 1차원

img

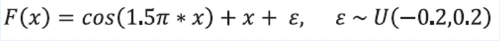
  • 이렇게 생긴 함수를 학습하기 위해 다음과 같은 뉴럴넷 구조를 사용한다.

img

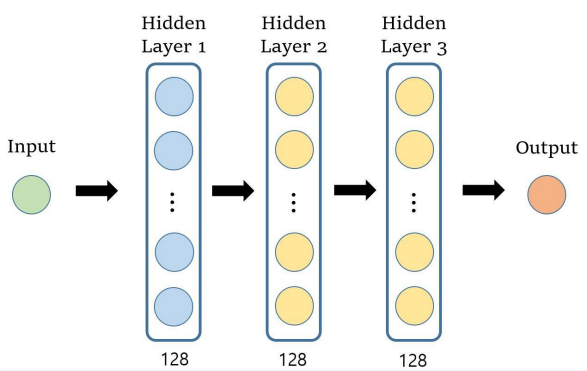
  • 총 3개의 레이어가 있고 각 레이어는 128개의 노드가 포함되어있습니다.

라이브러리 import

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

Model 클래스

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.fc1 = nn.Linear(1, 128)
        self.fc2 = nn.Linear(128, 128)
        self.fc3 = nn.Linear(128, 128)
        self.fc4 = nn.Linear(128, 1, bias=False)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.relu(self.fc3(x))
        x = self.fc4(x)
        return x

데이터 생성 함수 F(x)

def true_fun(X):
    noise = np.random.rand(X.shape[0]) * 0.4 - 0.2
    return np.cos(1.5 * np.pi * X) + X + noise

plotting 함수

def plot_results(model):
    x = np.linspace(0, 5, 100)
    input_x = torch.from_numpy(x).float().unsqueeze(1)
    plt.plot(x, true_fun(x), label="Truth")
    plt.plot(x, model(input_x).detach().numpy(), label="Prediction")
    plt.legend(loc='lower right',fontsize=15)
    plt.xlim((0, 5))
    plt.ylim((-1, 5))
    plt.grid()

메인 함수

def main():
    data_x = np.random.rand(10000) * 5 # 0~5 사이 숫자 1만개를 샘플링하여 인풋으로 사용 
    model = Model()
    optimizer = optim.Adam(model.parameters(), lr=0.001)

    for step in range(10000):
        batch_x = np.random.choice(data_x, 32) # 랜덤하게 뽑힌 32개의 데이터로 mini-batch를 구성
        batch_x_tensor = torch.from_numpy(batch_x).float().unsqueeze(1)
        pred = model(batch_x_tensor)

        batch_y = true_fun(batch_x)
        truth = torch.from_numpy(batch_y).float().unsqueeze(1)
        loss = F.mse_loss(pred, truth) # 손실 함수인 MSE를 계산하는 부분
        
        optimizer.zero_grad() 
        loss.mean().backward() # 역전파를 통한 그라디언트 계산이 일어나는 부분
        optimizer.step() # 실제로 파라미터를 업데이트 하는 부분

    plot_results(model)

if __name__ == '__main__':
    main()

학습 전 그래프

img

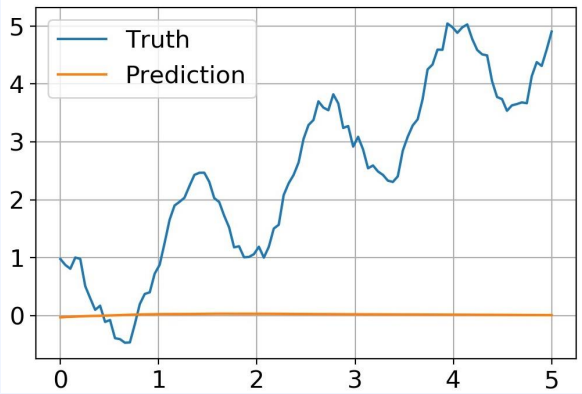
학습 후 그래프

img

Categories:

Updated:

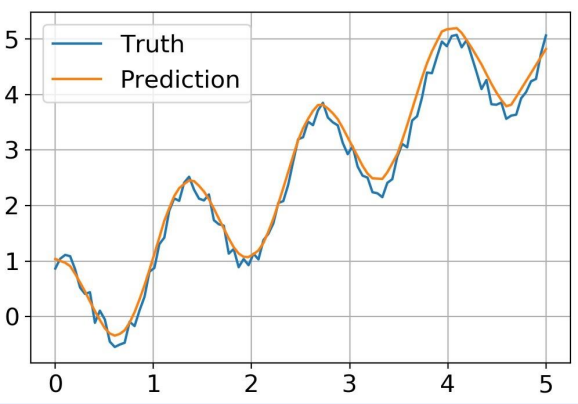
Leave a comment

You may also enjoy