강화학습 Chapter 7. Value 기반 에이전트
개요
- 신경망을 이용해 action value 네트워크를 학습하면 그게 곧 하나의 에이전트가 될 수 있다.
- 아타리 게임을 플레이 하던 DQN이 바로 이 방식
- value 함수만을 가지고 움직이는 에이전트, 즉 value 기반 에이전트에 대해 알아보자.
1. Value 네트워크의 학습
1-1. RL 에이전트의 분류
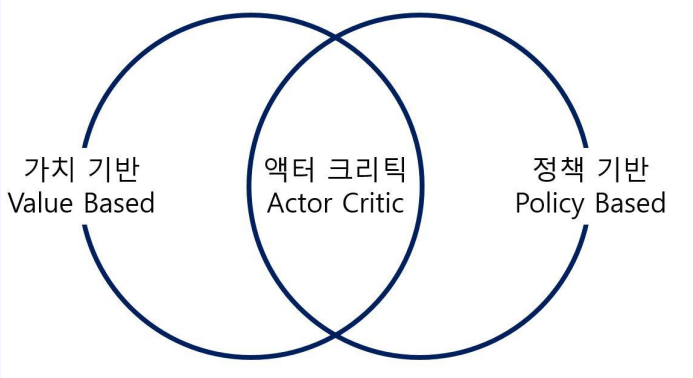
- 가치 기반 : $q(s,a)$ 갖고 행동
- 정책 기반 : $\pi(s)$ 갖고 행동
- 액터 크리틱 : 학습 도중 $\pi, v(or \ \ q)$ 둘다 사용됨
1-2. Value 네트워크
- 정책 $\pi$가 고정되어 잇을 때, 뉴럴넷을 이용하여 $\pi$의 가치 함수 $v_\pi(s)$를 학습하는 방법에 대해 배워보자.
- vlaue 함수($v_\theta$)를 뉴럴넷으로 표현한것이 Value 네트워크
- 뉴럴넷에 정답을 기록할 것
- $v_\theta(s)$로 표현, $\theta$는 뉴럴넷의 파라미터
정답이 주어져 있다고 가정하면
- 정답을 $v_{true}(s)$라고 가정
- 학습하기 위해선 Loss func을 정의 해야함
- Loss func
- $ L(\theta) = (v_{true}(s) - V_\theta(s))^2$
-
모든 상태에 대해 위 값을 구하기는 불가능하기 때문에 기댓값을 사용 \(L(\theta) = E_\pi[(v_{true}(s) - V_\theta(s))^2]\)
- $\theta$에 대한 gradient를 계산하면
- $\triangledown_\theta L(\theta) = -E_\pi[(v_{true}(s) - V_\theta(s))\triangledown_\theta v_\theta(s)]$
- 기댓값은 $\pi$ 에이전트가 지나간 $s$들을 이용해 구하면 된다.
- $\triangledown_\theta L(\theta) \approx -(v_{true}(s) - V_\theta(s))\triangledown_\theta v_\theta(s)$
- 결국 업데이트는 다음과 같이 된다.
-
$ \theta’ = \theta - \alpha\triangledown_\theta L(\theta) \ \ \ \ \ = \theta + \alpha(v_{true}(s) - v_\theta(s))\triangledown_\theta v_\theta(s)$
-
- 하지만 실제 상황에서는 정답이 주어질 일은 없다.
- 정답이 주어지지 않아도 구할 수 있는 방법 몇 가지를 알고 있다.
- MC return과 TD target입니다. 먼저 MC return 부터 알아보자.
1-3. Monte Carlo Return
- t시점에서 시작하여 에피소드가 끝날 때까지 얻은 감쇠된 누적 보상을 리턴 $G_t$로 표현 했다.
- 실제 가치 함수의 정의가 곧 $G_t$의 기댓값이기 때문에 $v_{true}$에 $G_t$를 사용할수있다.
- Loss func
- $ L(\theta) = E_\pi[(G_t - V_\theta(s))^2] $
- update
- $ \theta’ = \theta + \alpha(G_t - v_\theta(s))\triangledown_\theta v_\theta(s)$
- MC의 특성은 그대로 남아 있다.
- 에피소드가 끝나야만 리턴을 계산할 수 있어 실시간으로 업데이트 불가능
- 에피소드가 끝날 때까지 많은 확률적 요소가 결합되어 있어서 정답지의 분산이 크다는 점
1-4. TD target
- 정답 자리에 $r_{t+1} + \gamma v_\theta(s_{t+1})$ 대입
- Loss func
- $ L(\theta) = E_\pi[(r_{t+1} + \gamma v_\theta(s_{t+1}) - V_\theta(s))^2] $
- update
- $ \theta’ = \theta + \alpha(r_{t+1} + \gamma v_\theta(s_{t+1}) - v_\theta(s))\triangledown_\theta v_\theta(s)$
- 주의할점
- 정답은 미분이 되면 안됨 ( 정답은 변하면 안됨 )
- 추측을 미분하면 추측은 정답 방향으로 움직인다.
- 정답을 미분하면 정답은 추측 방향으로 움직이기 때문
- 정답은 변수가 아닌 상수로 취급한다. 따라서 미분이 되는 $\gamma v_\theta(s_{t+1}) = 0$으로 만들어 버린다.
2. Deep Q Learning 이론
딥마인드 - DQN

- ATARI 게임을 DQN을 이용해 풀음
- 이미지를 input으로 넣어 action을 output으로 나타냄
- 딥 Q러닝은 뉴럴넷을 이용해 $q_*(s,a)$를 학습하고 싶은 것
- $q_\pi(s,a)$는 정해진 $\pi$를 따라 갈때의 Value
- $q_*(s,a)$는 optimal value
2-1. 이론적 배경
- Q 러닝($q(s,a)$)은 벨만 최적방정식을 이용하였다.
- 이제 테이블이 아닌 뉴럴넷을 이용하기 때문에 $Q(s,a)$으로 표현 합니다.
-
정답을 $ r+\gamma \max_{a’}Q(s’,a’) $
- Loss func
- $ L(\theta) = E[(r+\gamma \max_{a’}Q(s’,a’) - Q_\theta(s))^2] $
- update
- $ \theta’ = \theta + \alpha(r+\gamma \max_{a’}Q(s’,a’) - Q_\theta(s))\triangledown_\theta Q_\theta(s,a)$
2-2. 딥 Q러닝 pseudo code
- 뉴럴넷 ( $Q_\theta$ ), 파라미터( $\theta$ )
- $Q_\theta$의 파라미터 $\theta$를 초기화
- 에이전트의 상태 $s$를 초기화 ($s \leftarrow s_0$)
- 에피스드가 끝날 때까지 다음을 반복
- $Q_\theta$에 대한 $\epsilon - greedy$를 이용하여 액션 $a$를 선택
- $a$를 실행하여 환경이 주는 $r$과 다음상태($s’$)을 관측
- $s’$에서 $Q_\theta$에 대한 greedy를 이용하여 액션 $a’$을 선택
- $\theta$ 업데이트 : $ \theta \leftarrow \theta + \alpha(r+\gamma \max_{a’}Q(s’,a’) - Q_\theta(s))\triangledown_\theta Q_\theta(s,a)$
- $s \leftarrow s’$
- 에피소드가 끝나면 다시 2번으로 돌아가서 $\theta$가 수렴할 때까지 반복
- 3번의 $Q_\theta$에 대한 $\epsilon - greedy$를 이용하여 액션 $a$를 선택은
- Q값이 제일 높은 확률을 뽑다가 $\epsilon$ 이라는 작은 확률로 랜덤하게 액션을 뽑는걸 서로 섞어 주는 것을 말한다.
- 3번의 $s’$에서 $Q_\theta$에 대한 greedy를 이용하여 액션 $a’$을 선택
- 여기서 선택한 $a’$은 실제로 실행되자는 않으며, 업데이트를 위한 계산에만 사용되는 부분
- 다음으로는 이 학습에 안정화를 주기 위해 두가지 기법이 들어간다.
2-3. Experience Replay
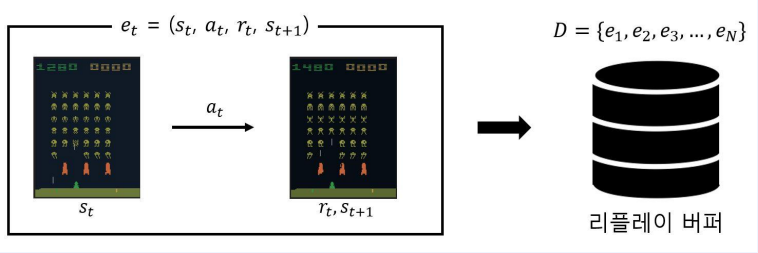
- “겪었던 경험을 재사용하면 더 좋지 않을까?”하는 아이디어에서 출발했다.
- 경험은 려어개의 에피소드로 이루어져 있고, 에피소드는 여러 개의 상태 전이(transition)로 이루어져 있다.
- 하나의 상태 전이$e_t$는 $(s_t,a_t, r_t,s_{t+1})$로 표현
- $s_t$에서 $a_t$를 했더니 $r_t$를 받고 $s_{t+1}$에 도착했다.
- 이러한 데이터를 재사용하기 위해 Replay buffer라는 개념을 도입한다.
- 버퍼에다가 가장 최근의 데이터 n개를 저장해 놓자는 아이디어
- 해당 논문에서는 데이터 100만개를 저장하고 임의로 데이터 32개씩 뽑아서 미니 배치를 만들어 학습하는 방식을 사용
장점
- 데이터를 재사용하여 효율성을 올려줌
- 임의의 데이터를 뽑게 되면 서로 다른 게임에서 발생한 다양한 데이터들이 마구 섞이게 된다. 그러면 산 게임 안에서 발생한 연속된 데이터를 사용할 때 보다 각각의 데이터 사이의 상관성이 작아서 더 효율적으로 학습할 수 있다.
- 즉 데이터 사이의 상관성을 줄여주는 장점이 있다는 것이다.
주의할점
- off-policy 알고리즘에만 사용할 수 있다.
- 해당 데이터를 생성한 정책과 현재 학습을 받고 있는 타깃 정책이 서로 다른 정책이기 때문
2-4. Target Network
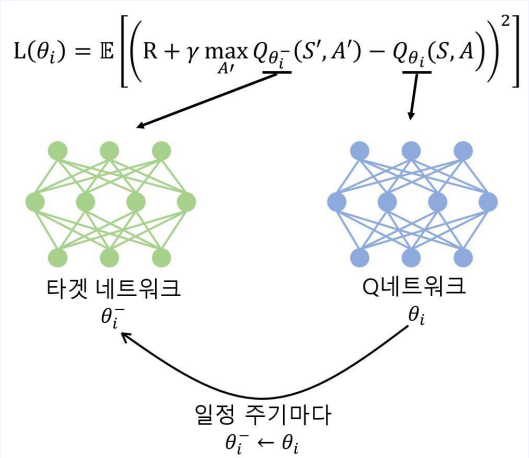
- DQN의 loss를 자세히 보면 추측치와 정답지가 함께 변함
- 정답지는 장 안바뀌면 좋음
- 그렇다고 너무 안 바뀌면 학습의 의미가 없음
- 일정 주기마다 바꿔주자
- 네트워크 1000번 업데이트 동안 정답지는 바꿔주지 않는 식

Leave a comment