강화학습 Chapter 8. Policy 기반 에이전트
개요
- 보상 및 Value 네트워크를 이용해 직접적으로 Policy 네트워크를 학습하는 방법에 대해 알아보자
- 수많은 최신 강화 학습 알고리즘의 뿌리가 되는 방법론
1. Policy Gradient Theorem
1-1. Policy 기반 에어전트가 필요한 경우
- 확률적 액션이 필요한 경우
- action space가 continuous인 경우
- $ a \in [0,1] $
- $Q(s,a)$를 최대로 하는 $a$를 찾는 문제
1-2. 목적 함수 정하기
- 정책 네트워크 : $ \pi_\theta (s)$
- 우리가 원하는 것
- reward를 많이 받는 것
- -> 큰 리턴을 받는 것
- -> 큰 리턴의 기댓값을 받는 것
- -> Value가 높은 것
- -> 첫 상태 $s_0$의 Value가 높은 것
-
목적함수 : $ J(\theta) = v_{\pi _\theta} (s_0)$
- $ J(\theta) $를 늘릴려면 $\theta$에 대해 gradient ascent를 하면 됨
- $ \theta’ \gets \theta + \alpha * \nabla _\theta J(\theta)$
- 그렇다면 $\nabla _\theta J(\theta)$(Policy gradient)는 어떻게 구하나
- 먼저 1-step MDP의 예로 알아보자
1-step MDP
- 1-step MDP는 $s_0$에서 액션 $a$ 한번 선택 후, reward를 받고 종료되는 MDP
- 첫 상태 $s_0$의 분포를 $d(s)$로 하자
- 첫 상태가 하나가 아닌 랜덤하게 여러개 일 수 있으니
- 그러면 다음이 성립
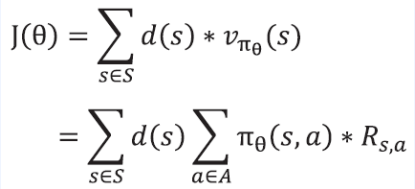
- 하지만 이 값은 구하는 것이 불가능함
- $ R_{s,a} $를 모름
- 또한 모든 상태의 S에 대해서 연결이 된 모든 A에 대해서 그때의 확률과 보상을 다 관측할 수 없기 때문
- 그래서 다시 한번 더 식을 변형을 하자
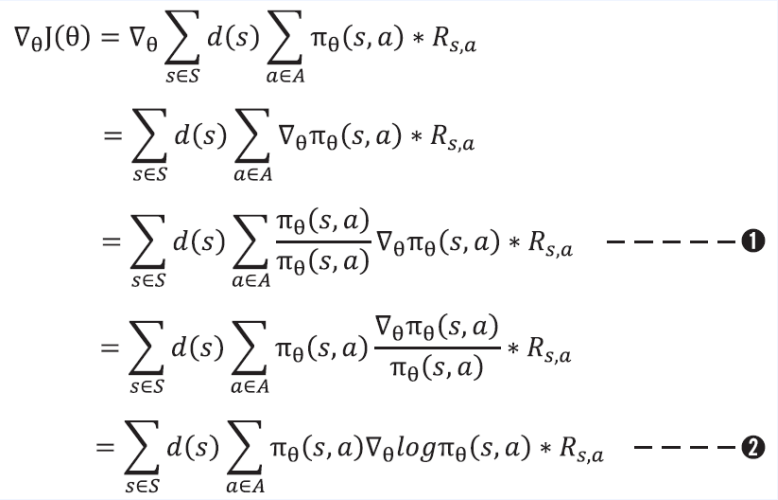
- 다음으로 샘플 기반 방법론을 사용하자
- 식을 $\pi$에 대한 기댓값 형태로 바꾸자
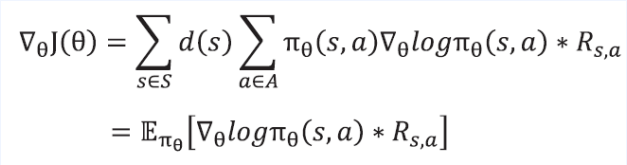
- $ \pi _ \theta $ 를 이용해 경험을 쌓고 그 경험을 이용해 괄호 안인 $ \nabla \theta log\pi _\theta(s,a) * R{s,a} $ 를 계산 하고 이를 평균 내면 됨
- 일반적인 MDP로 확장해서 최종 식을 완성
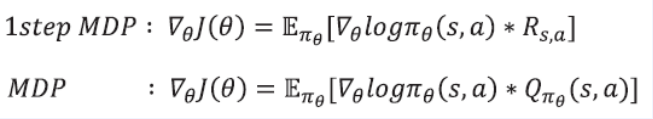
- 다음으로는 Policy Gradient Theorem을 기반으로 하는 REINFORCE 알고리즘을 알아보자
2. REINFORCE
- Policy gradient 알고리즘 중 가장 기본적이고, 고전적이면서도 간단한 알고리즘
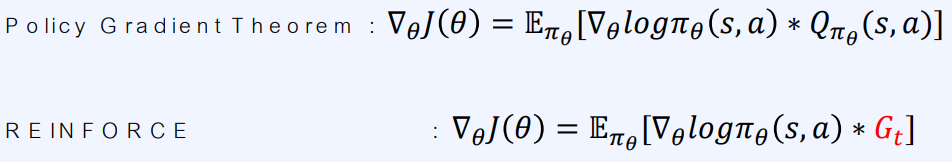
- $ Q_{\pi _\theta} $ 대신 $G_t$가 쓰이는 것이 전부
- $G_t$가 $Q$의 샘플이기 때문
2-1. REINFORCE의 pseudo code

- A. 에이전트를 처음 상태로 초기화
- B. $\pi _\theta$를 따라 에피소드를 끝까지 진행
- C. $ G_t $를 구하고 $\theta$를 업데이트
직관적으로 의미를 알아보자
- $ \alpha = 0.0001 $
-
$ \theta’ \gets \theta + \alpha * \nabla _\theta log\pi _\theta(s,a) * G_t$
- 여기서 $G_t$가 없다면?
- $ \nabla _\theta log\pi _\theta(s,a) $는 $\pi _\theta(s,a) $를 증가 시키는 방향과 같음
- 더 정확히는 $ log\pi _\theta(s,a) $ 를 증가 시키는 방향
- $log$ 함수는 단조증가 함수
- $ G_t $가 다음 값일 경우를 생각해보자
- -1 : $ \theta $ 를 반대방향으로 움직임
- +100 : $ \theta $ 를 100배 더 움직임
- 따라서 간단하게 정리를 하면
- 현재 상태에서 미래 리턴의 값이 양수이면 액션의 확률을 높여주고
- 반대로 현재 상태에서 미래 리턴의 값이 음수이면 액션의 확률을 낮춰 주는 것
- 아주 무식한 방법이지만 알파고를 학습할 때 쓰였음
2-2. 실제 구현시 주의 할 것
\[Loss = -log\pi _\theta (s,a) * G_t\]- Loss를 다음과 같이 구현 할 것
3. 액터 크리틱
3-1. 세 가지 종류의 액터 크리틱
- 다음과 같이 세 가지가 있다
- Q 액터 크리틱
- 어드백티지 액터 크리틱
- TD 액터 크리틱
- Policy Gradient Theorem : \(\nabla _\theta J(\theta) = E_{\pi _\theta}[\nabla _\theta log\pi _\theta (s,a) * Q_{\pi _\theta}(s,a)]\)
- 여기서 $ Q_{\pi _\theta}(s,a) $에 무엇이 들어가냐의 차이
3-2. Q 액터 크리틱
- 액터 크리틱은 다음 두 요소를 함께 학습하는 것
- Policy : $\pi(s)$
- Value : $q_\pi(s,a)$ or $v_\pi(s)$
- Policy Gradient Theorem에서 Q함수는 모른기 때문에 같이 학습
- 따라서 네트워크가 두개가 필요하다
- $Q_{\pi _\theta}$를 학습하는 것 ( 크리틱 )
- $\pi$를 학습하는 것 ( 액터 )
- 표현은 $Q_{\pi _\theta} = Q_w, \ \ \ \pi = \theta$
Q 액터 크리틱의 pseudo code

3-3. 어드밴티지 액터 크리틱
- Policy Gradient Theorem : \(\nabla _\theta J(\theta) = E_{\pi _\theta}[ \nabla _\theta log\pi _\theta(s,a) * Q_{\pi _\theta}(s,a)]\)
- $\nabla _\theta log\pi _\theta(s,a)$ 은 벡터
- $Q_{\pi _\theta}(s,a)$ 은 숫자
- 좋은 상태 $s’$에 도착했고 그 Value를 안다고 가정
- $Q_{\pi _\theta}(s,a_0) = 1000$
- $Q_{\pi _\theta}(s,a_1) = 1050$
- Q 액터 크리틱에서는 둘다 값이 크기 때문에 업데이트 또한 크게 일어남
- 결국 둘은 같이 확률이 높아짐 하지만 $a_0$보단 $a_1$이 더 좋음 그렇다면 $a_1$만 확률을 높여야 더 효율적이지 않나? 라는 질문에서 시작됨
- 식을 다음과 같이 바꾸자 ( $ V_{\pi _\theta}(s) $ 를 추가 )
- 의미를 보자면 s에서 a를 하는 것이 얼만큼 더 좋으냐가 됨
- 즉 앞선 예에서 $a_0 = 1000, \ \ \ a_1 = 1050, \ \ \ V_{\pi _\theta}(s) = 1025 $라고 가정하면
- $a_0 = -25, \ \ \ a_1 = 25$가 되어서 둘의 차이가 발생하게 됨
- 이것이 어드밴티지
- 여기서 $ V_{\pi _\theta}(s) $를 뺄 수 있으려면 다음이 성립 해야됨
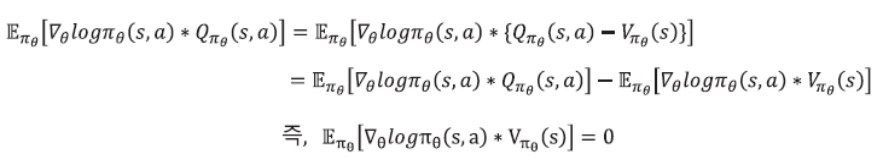
- 증명을 따로 적지는 않지만 이것은 성립이 됨
- 따라서 최종적으로 얻는 식은 다음과 같다
\(\nabla _\theta J(\theta) = E_{\pi _\theta}[ \nabla _\theta log\pi _\theta(s,a) * A_{\pi_\theta}(s,a)]\) \(A_{\pi_\theta}(s,a) \equiv Q_{\pi _\theta}(s,a) - V_{\pi _\theta}(s)\)
- 결국 학습하기 위해서는 3개의 네트워크가 필요
- 정책함수 $\pi_theta(s,a)$의 뉴럴넷 $\theta$
- 액션-가치 함수 $Q_w(s,a)$의 뉴럴넷 $w$
- 가치 함수 $V_\phi(s)$의 뉴럴넷 $\phi$
어드밴티지 액터 크리틱의 pseudo code

3-4. TD 액터 크리틱
- 어드밴티지의 단점은 세 개의 네트워크가 필요
- TD 액터 크리틱은 $Q_w$ 없이도 어드밴티지 기반 학습을 가능케 함
- 먼저 가치함수 $V(s)$의 TD 에러 $\delta$를 생각해보자
- $ \delta = r + \gamma * V(s’) - V(s) $
- s에서 a를 실행했을 때 $\delta$ 의 기댓값
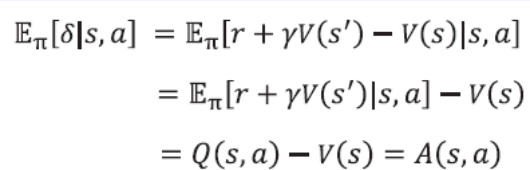
- $A(s,a)$ 자리에 $\delta$가 들어가도 된다는 뜻
변경 전
\[A_{\pi_\theta}(s,a) \equiv Q_{\pi _\theta}(s,a) - V_{\pi _\theta}(s)\]변경 후
\[A_{\pi_\theta}(s,a) \equiv Q_{\pi _\theta}(s,a) - \delta\]- $\delta$는 V(s)만 있으면 계산 가능
TD 액터 크리틱의 pseudo code

4. 배운 내용 정리


Leave a comment